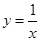题目内容
函数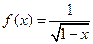 的定义域为
的定义域为
| A.{x|x>1} | B.{x|x<1} | C.{x|-1<x<1} | D.Æ |
B
解析

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知f(x)是偶函数,x ÎR,若将f(x)的图象向右平移一个单位又得到一个奇函
数,又f(2)=-1,则f(1)+ f(2)+ f(3)+…+ f(2011)= ( )
| A.-1003 | B.1003 | C.1 | D.-1 |
已知函数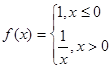 ,则使方程
,则使方程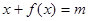 有解的实数
有解的实数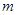 的取值范围
的取值范围
是( )
| A.(1,2) | B. | C.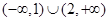 | D.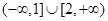 |
用min{a,b,c}表示a,b,c三个数中的最小值。设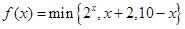
(x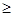 0),则
0),则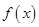 的最大值为 ( )
的最大值为 ( )
| A.4 | B.5 | C.6 | D.7 |
定义在R上的偶函数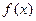 在
在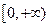 上递增,
上递增,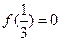 ,则满足
,则满足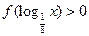 的
的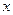 的取值范围是( )
的取值范围是( )
A.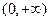 | B.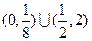 | C.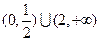 | D.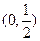 |
若函数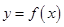 为偶函数,则函数
为偶函数,则函数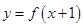 的一条对称轴是
的一条对称轴是
A.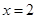 | B.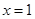 | C.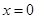 | D.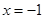 |
函数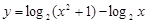 的值域是
的值域是
A.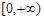 | B.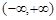 |
C.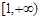 | D.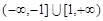 |
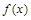 都满足不等式
都满足不等式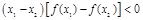 ,若函数
,若函数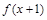 为奇函数,则不等式
为奇函数,则不等式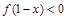 的解集为 ( )
的解集为 ( )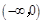

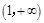
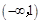
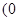 ,
,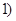 上是减函数的是 ( )
上是减函数的是 ( )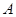 .
.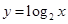
 .
. 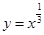
 .
.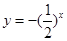
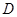 .
.