题目内容
已知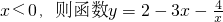
有
- A.最小值
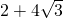
- B.最大值
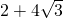
- C.最小值
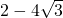
- D.最大值
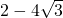
A
分析：因为x＜0，所以要先调整符号，转化为y=2+（-3x）+（-
），再利用均值不等式求解．
解答：∵x＜0，
∴y=2+（-3x）+（-）≥2+2
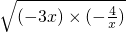=2+4
，
当且仅当-3x=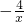
，即x=
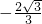时取等号．
故选A．
点评：在利用基本不等式时，要特别注意未知数的取值范围，只有满足一正、二定、三相等时，均值不等式才成立．
分析：因为x＜0，所以要先调整符号，转化为y=2+（-3x）+（-
），再利用均值不等式求解．解答：∵x＜0，
∴y=2+（-3x）+（-
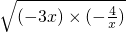）≥2+2=2+4，当且仅当-3x=
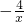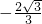，即x=时取等号．故选A．
点评：在利用基本不等式时，要特别注意未知数的取值范围，只有满足一正、二定、三相等时，均值不等式才成立．
练习册系列答案
相关题目
=1,则xy有( )
，则f(x)=
有( )
B.最小值
,则f(x)=
有( )
B.最小值
C.最大值1 D.最小值1
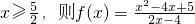有