题目内容
已知a,b,l表示三条不同的直线,α,β,γ表示三个不同的平面,有下列命题:
①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;
②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则α∥β;
③若α⊥β,α∩β=a,b在β内,a⊥b,则b⊥α;
④若a在α内,b在α内,l⊥a,l⊥b,则l⊥α.
其中正确的有( )
①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;
②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则α∥β;
③若α⊥β,α∩β=a,b在β内,a⊥b,则b⊥α;
④若a在α内,b在α内,l⊥a,l⊥b,则l⊥α.
其中正确的有( )
分析:①利用面面平行的判定定理进行判断.②利用面面平行的判定定理判断.③利用面面垂直和线面垂直的定义判断.④利用线面垂直判定定理判断.
解答:解:①如图,若平面ABCD∩平面ABFE=AB,平面ABFE∩平面CDEF=EF,AB∥EF,但平面ABCD与平面CDEF不平行.所以①错误.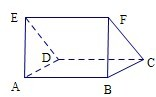
②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则a,b所在的平面γ满足γ∥α,γ∥β,所以必有α∥β成立,所以②正确.
③根据面面垂直的性质定理可知,若α⊥β,α∩β=a,b在β内,a⊥b,则b⊥α,所以③正确.
④根据线面垂直的判定定理可知,直线a,b必须是相交直线时,结论才成立,所以④错误.
故正确的是②③,
故选C.

②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则a,b所在的平面γ满足γ∥α,γ∥β,所以必有α∥β成立,所以②正确.
③根据面面垂直的性质定理可知,若α⊥β,α∩β=a,b在β内,a⊥b,则b⊥α,所以③正确.
④根据线面垂直的判定定理可知,直线a,b必须是相交直线时,结论才成立,所以④错误.
故正确的是②③,
故选C.
点评:本题主要考查空间直线和平面,平面和平面平行或垂直的性质和判断,要求熟练掌握相应的判定定理和性质定理即可.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 表示三个不同的平面,有下列四个命题:
表示三个不同的平面,有下列四个命题: 且
且 则
则 ;
; 外,
外, ,则
,则 ;
; ,
, 则
则 ;
; 则
则 .
.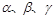 表示三个不同的平面,有下列四个命题:
表示三个不同的平面,有下列四个命题: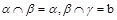 且
且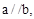 则
则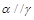 ;
;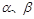 外,
外,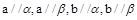 ,则
,则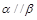 ;
;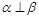 ,
,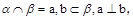 则
则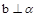 ;
;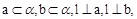 则
则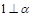 .
.