题目内容
已知函数y=x
,(1)求定义域;(2)判断奇偶性;(3)已知该函数在第一象限的图象如图所示,试补全图象,并由图象确定单调区间.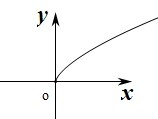
| 2 | 3 |

分析:根据幂函数的性质分别求出函数的定义域和奇偶性.
解答:解:(1)∵函数y=x
=
,∴函数的定义域为R.
(2)∵f(-x)=
=
=f(x),∴函数y=x
=
是偶函数.
(3)∵函数y=x
=
是偶函数.
∴函数图象关于y轴对称,且(-∞,0]为减函数,[0,+∞)为增函数,
对应的图象为:
| 2 |
| 3 |
| 3 | x2 |

(2)∵f(-x)=
| 3 | (-x)2 |
| 3 | x2 |
| 2 |
| 3 |
| 3 | x2 |
(3)∵函数y=x
| 2 |
| 3 |
| 3 | x2 |
∴函数图象关于y轴对称,且(-∞,0]为减函数,[0,+∞)为增函数,
对应的图象为:
点评:本题主要考查幂函数的图象和性质,要求熟练掌握幂函数的图象和性质以及函数奇偶性的判断.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目