题目内容
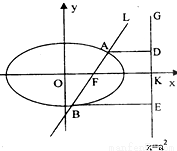
如图,已知直线L: 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.(1)若抛物线
 的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;
的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由.
(文科生做)若
 为x轴上一点,求证:
为x轴上一点,求证: .
.
【答案】分析:(1)先由已知得b= 以及c=1,即可求出椭圆C的方程;
以及c=1,即可求出椭圆C的方程;
(2)(理科生做)先让m取0,求出点N的坐标,再猜想:当m变化时,AE与BD相交于此定点N.先利用斜率相等证明A、N、E三点共线同理可得B、N、D三点共线,即可证明结论.
(文科生做)直接求直线AN和直线NE的斜率,利用上面的过程得到二者斜率相等即可证明结论.
解答:解:(1)易知b= ⇒b2=3,
⇒b2=3,
又F(1,0),c=1,∴a2=b2+c2=4.
所以椭圆C的方程为: =1.
=1.
(2)(理科生做)因为F(1,0),k=(a2,0)
先探索,当m=0时,直线L⊥ox轴,则ABED为矩形,由对称性知,AE与BD相交于FK中点N,且
猜想:当m变化时,AE与BD相交于定点 .
.
证明:设设A(x1,y1),B(x2,y2),E(a2,y2),D(a2,y1),
当m变化时首先AE过定点N.
由 ⇒(a2+b2m2)y2+2mb2y+b2(1-a2)=0.△4a2b2(a2+m2b2-1)>0,(因为a>1)
⇒(a2+b2m2)y2+2mb2y+b2(1-a2)=0.△4a2b2(a2+m2b2-1)>0,(因为a>1)
且.y1+y2=- ①,y1•y2=
①,y1•y2=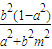 ②.
②.
因为KAN= ,KEN=
,KEN= ,
,
所以kAN-KEN= ③,
③,
把①②代入③整理得KAN-KEN=0.
∴KAN=KEN∴A、N、E三点共线同理可得B、N、D三点共线
∴AE与BD相交于定点 .
.
(文科生做).直接求出直线AN和直线NE的斜率,利用上面的推导过程可以得到二者斜率相等,故A、N、E三点共线.即可得: .
.
点评:题主要考查椭圆的标准方程,直线与椭圆的位置关系以及直线和直线之间的关系等基础知识,考查推理论证能力,运算求解能力及创新意识,考查化归与转化思想,数形结合思想以及特殊与一般思想.
 以及c=1,即可求出椭圆C的方程;
以及c=1,即可求出椭圆C的方程;(2)(理科生做)先让m取0,求出点N的坐标,再猜想:当m变化时,AE与BD相交于此定点N.先利用斜率相等证明A、N、E三点共线同理可得B、N、D三点共线,即可证明结论.
(文科生做)直接求直线AN和直线NE的斜率,利用上面的过程得到二者斜率相等即可证明结论.
解答:解:(1)易知b=
 ⇒b2=3,
⇒b2=3,又F(1,0),c=1,∴a2=b2+c2=4.
所以椭圆C的方程为:
 =1.
=1.(2)(理科生做)因为F(1,0),k=(a2,0)
先探索,当m=0时,直线L⊥ox轴,则ABED为矩形,由对称性知,AE与BD相交于FK中点N,且

猜想:当m变化时,AE与BD相交于定点
 .
.证明:设设A(x1,y1),B(x2,y2),E(a2,y2),D(a2,y1),
当m变化时首先AE过定点N.
由
 ⇒(a2+b2m2)y2+2mb2y+b2(1-a2)=0.△4a2b2(a2+m2b2-1)>0,(因为a>1)
⇒(a2+b2m2)y2+2mb2y+b2(1-a2)=0.△4a2b2(a2+m2b2-1)>0,(因为a>1)且.y1+y2=-
 ①,y1•y2=
①,y1•y2=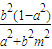 ②.
②.因为KAN=
 ,KEN=
,KEN= ,
,所以kAN-KEN=
 ③,
③,把①②代入③整理得KAN-KEN=0.
∴KAN=KEN∴A、N、E三点共线同理可得B、N、D三点共线
∴AE与BD相交于定点
 .
.(文科生做).直接求出直线AN和直线NE的斜率,利用上面的推导过程可以得到二者斜率相等,故A、N、E三点共线.即可得:
 .
.点评:题主要考查椭圆的标准方程,直线与椭圆的位置关系以及直线和直线之间的关系等基础知识,考查推理论证能力,运算求解能力及创新意识,考查化归与转化思想,数形结合思想以及特殊与一般思想.

练习册系列答案
相关题目

 如图,已知直线L:
如图,已知直线L: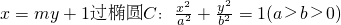 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.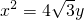 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;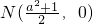 为x轴上一点,求证:
为x轴上一点,求证: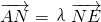 .
. 如图,已知直线L:
如图,已知直线L: 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E. 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程; 为x轴上一点,求证:
为x轴上一点,求证: .
.