题目内容
函数 的定义域为
的定义域为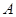 ,若存在非零实数
,若存在非零实数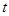 ,使得对于任意
,使得对于任意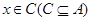 有
有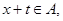 且
且 ,则称
,则称 为
为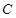 上的
上的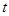 度低调函数.已知定义域为
度低调函数.已知定义域为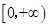 的函数
的函数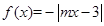 ,且
,且 为
为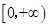 上的
上的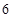 度低调函数,那么实数
度低调函数,那么实数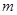 的取值范围是( )
的取值范围是( )
A.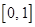 | B.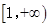 | C.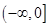 | D.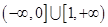 |
D
解析试题分析:由题意得,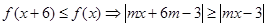 对任意
对任意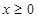 都成立.当
都成立.当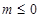 时,
时,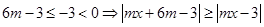 恒成立;当
恒成立;当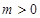 时,结合图象可知,要
时,结合图象可知,要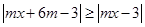 对任意
对任意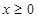 都成立,只需
都成立,只需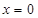 时
时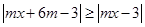 成立即可,即
成立即可,即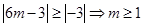 .选D.
.选D.
考点:1、新定义函数;2、绝对值不等式.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
设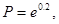
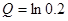 ,
,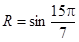 ,则( )
,则( )
A.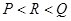 | B.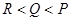 | C.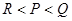 | D.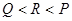 |
某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是( )
| A.118元 | B. 105元 | C. 106元 | D. 108元 |
设函数 ,若
,若 则
则 ( )
( )
A. | B.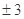 | C.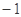 | D. |
若函数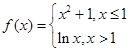 则
则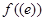 (e为自然对数的底数)=( )
(e为自然对数的底数)=( )
| A.0 | B.1 | C.2 | D.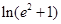 |
函数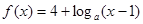 (a>0,且a≠1)的图像过一个定点,则这个定点坐标是( )
(a>0,且a≠1)的图像过一个定点,则这个定点坐标是( )
| A.(2,5) | B.(4,2) | C.(2,4) | D.(1,4) |
已知函数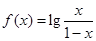 ,若
,若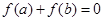 且
且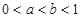 ,则
,则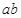 的取值范围是( )
的取值范围是( )
A.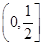 | B.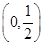 | C.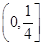 | D.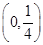 |
设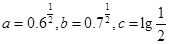 ,则
,则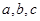 之间的关系是 ( )
之间的关系是 ( )
A.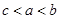 | B.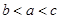 | C.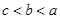 | D.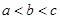 |
已知关于 的方程
的方程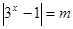 有一解,则
有一解,则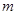 的取值范围为( )
的取值范围为( )
A.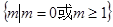 | B.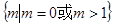 | C.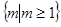 | D.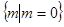 |