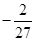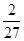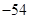题目内容
已知函数 是常数
是常数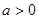 且
且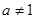 )在区间
)在区间 上有
上有
(1)求 的值;
的值;
(2)若 当
当 时,求
时,求 的取值范围;
的取值范围;
 是常数
是常数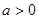 且
且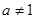 )在区间
)在区间 上有
上有
(1)求
 的值;
的值;(2)若
 当
当 时,求
时,求 的取值范围;
的取值范围;⑴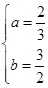 或
或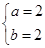 ;⑵
;⑵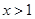 或
或 .
.
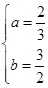 或
或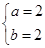 ;⑵
;⑵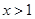 或
或 .
.试题分析:⑴先求出指数
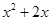 的取值区间,然后根据指数函数的性质对
的取值区间,然后根据指数函数的性质对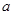 进行讨论,根据指数函数的性质判断函数的单调性,与最值结合即能解出参数的值;⑵根据参数的取值集合先确定参数的具体值,代入不等式根据指数函数的单调性解不等式即可.
进行讨论,根据指数函数的性质判断函数的单调性,与最值结合即能解出参数的值;⑵根据参数的取值集合先确定参数的具体值,代入不等式根据指数函数的单调性解不等式即可.试题解析:(1)因为
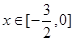 ,∴
,∴ 值域为
值域为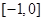 ,即
,即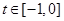 , 2分
, 2分若
 ,函数
,函数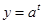 在
在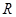 上单调递增,
上单调递增,所以,
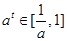 则
则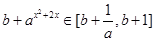 ,
,
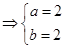 , .4分
, .4分若
 ,函数
,函数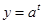 在
在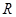 上单调递减,
上单调递减,所以
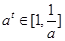 则
则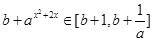 ,
,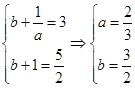 , .6分
, .6分所求
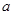 ,
,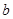 的值为
的值为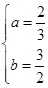 或
或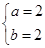 ; 7分
; 7分(2)由(1)可知
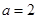 ,
,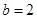 , ..8分
, ..8分则
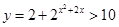 ,得
,得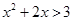 即
即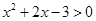 ,
,解得
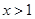 或
或 . .12分
. .12分
练习册系列答案
相关题目
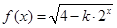 在
在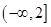 上有意义,则实数
上有意义,则实数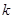 的取值范围是_ ___.
的取值范围是_ ___.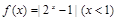 则关于
则关于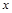 的方程
的方程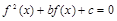 有
有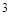 个不同实数解的充分条件是( )
个不同实数解的充分条件是( ) 且
且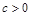
 且
且
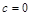
 且
且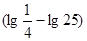 ÷
÷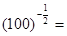 ____________.
____________.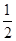 ,则化简
,则化简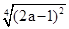 的结果是( )
的结果是( )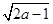
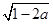
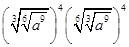 等于( )
等于( )



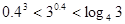



 的值为( )
的值为( )