题目内容
命题p:关于 的不等式
的不等式 对于一切
对于一切 恒成立,命题q:函数
恒成立,命题q:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围;
【答案】
设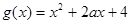 ,由于关于
,由于关于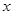 的不等式
的不等式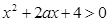 对于一切
对于一切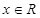 恒成立,所以函数
恒成立,所以函数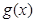 的图象开口向上且与
的图象开口向上且与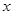 轴没有交点,故
轴没有交点,故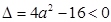 ,∴
,∴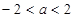 .
.
 2分
2分
函数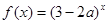 是增函数,则有
是增函数,则有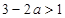 ,即
,即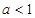 .
.
由于p或q为真,p且q为假,可知p、q一真一假.
① 若p真q假,则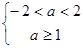 ∴
∴ ;
;
② p假q真,则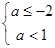
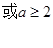 ∴
∴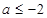 ;
;
综上可知,所求实数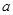 的取值范围是{
的取值范围是{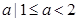 或
或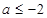 }
}
【解析】略

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
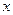 的不等式
的不等式 ,
, 恒成立;
恒成立;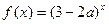 是增函数,
是增函数, 是真命题,求实数
是真命题,求实数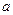 的取值范围.
的取值范围. 的不等式
的不等式 ,
,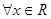 恒成立;
恒成立;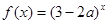 是增函数,
是增函数, 是真命题,求实数
是真命题,求实数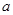 的取值范围.
的取值范围. 的不等式
的不等式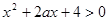 对于一切
对于一切 恒成立,命题q:指数
恒成立,命题q:指数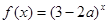 是增函数,若
是增函数,若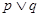 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围;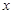 的不等式
的不等式 对一切
对一切 恒成立,命题q:函数
恒成立,命题q:函数 是增函数,若p或q为真,p且q为假,求实数
是增函数,若p或q为真,p且q为假,求实数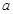 的取值范围.
的取值范围.