题目内容
已知等差数列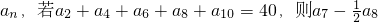 的值为
的值为
- A.1
- B.2
- C.3
- D.4
D
分析:利用等差数列的性质和通项公式,将a2+a4+a6+a8+a10用a1和d表示,再将a7- a8用a1和d表示,从中寻找关系求解.
a8用a1和d表示,从中寻找关系求解.
解答:∵{an}为等差数列,设首项为a1,公差为d,
∴a2+a4+a6+a8+a10=5a6=5a1+25d=40;
∴a1+5d=8,
∴a7- a8=a1+6d-(
a8=a1+6d-( a1+
a1+ d)=
d)= (a1+5d)=4;
(a1+5d)=4;
故选D.
点评:本题考查了等差数列的性质和通项公式,用到了基本量a1与d,还用到了整体代入思想.
分析:利用等差数列的性质和通项公式,将a2+a4+a6+a8+a10用a1和d表示,再将a7-
 a8用a1和d表示,从中寻找关系求解.
a8用a1和d表示,从中寻找关系求解.解答:∵{an}为等差数列,设首项为a1,公差为d,
∴a2+a4+a6+a8+a10=5a6=5a1+25d=40;
∴a1+5d=8,
∴a7-
 a8=a1+6d-(
a8=a1+6d-( a1+
a1+ d)=
d)= (a1+5d)=4;
(a1+5d)=4;故选D.
点评:本题考查了等差数列的性质和通项公式,用到了基本量a1与d,还用到了整体代入思想.

练习册系列答案
相关题目
 的公差为2 , 若
的公差为2 , 若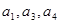 成等比数列, 则
成等比数列, 则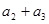 的值为( )
的值为( )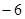 B.
B.
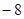 C.
C.
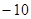 D.
D.
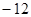
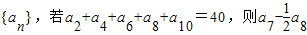 的值为( )
的值为( )