题目内容
已知 的展开式中x3的系数为
的展开式中x3的系数为 ,则关于t的不等式at2-4t-3<0的解集为 .
,则关于t的不等式at2-4t-3<0的解集为 .
【答案】分析:在 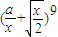 的展开式的通项公式中,令x的系数等于3,求得
的展开式的通项公式中,令x的系数等于3,求得  的展开式中x3的系数,根据它等于
的展开式中x3的系数,根据它等于 ,求出a的值,解关于t的不等式at2-4t-3<0,求出其解集.
,求出a的值,解关于t的不等式at2-4t-3<0,求出其解集.
解答:解:由于 的展开式的通项公式为 Tr+1=
的展开式的通项公式为 Tr+1=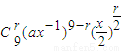 =
=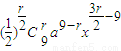 ,令
,令 r-9=3,可得 r=8.
r-9=3,可得 r=8.
故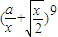 的展开式中x3的系数为
的展开式中x3的系数为  =
=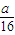 =
= ,∴a=4.
,∴a=4.
则关于t的不等式at2-4t-3<0 即 4t2-4t-3<0,∴- <t<
<t< ,故不等式的解集为
,故不等式的解集为 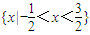 ,
,
故答案为: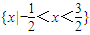 .
.
点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,一元二次不等式的解法,属于中档题.
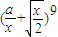 的展开式的通项公式中,令x的系数等于3,求得
的展开式的通项公式中,令x的系数等于3,求得  的展开式中x3的系数,根据它等于
的展开式中x3的系数,根据它等于 ,求出a的值,解关于t的不等式at2-4t-3<0,求出其解集.
,求出a的值,解关于t的不等式at2-4t-3<0,求出其解集.解答:解:由于
 的展开式的通项公式为 Tr+1=
的展开式的通项公式为 Tr+1=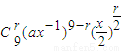 =
=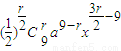 ,令
,令 r-9=3,可得 r=8.
r-9=3,可得 r=8.故
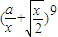 的展开式中x3的系数为
的展开式中x3的系数为  =
=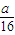 =
= ,∴a=4.
,∴a=4.则关于t的不等式at2-4t-3<0 即 4t2-4t-3<0,∴-
 <t<
<t< ,故不等式的解集为
,故不等式的解集为 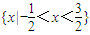 ,
,故答案为:
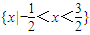 .
.点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,一元二次不等式的解法,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 的展开式中x3的系数为
的展开式中x3的系数为 ,常数a的值为 .
,常数a的值为 . 的展开式中x3的系数为
的展开式中x3的系数为 ,常数a的值为 .
,常数a的值为 . 的展开式中x3的系数为
的展开式中x3的系数为 ,常数a的值为 .
,常数a的值为 . 的展开式中x3的系数为
的展开式中x3的系数为 ,常数a的值为 .
,常数a的值为 .