题目内容
如果一个三位正整数形如“a1a2a3”满足a1<a2且a3<a2,则称这样的三位数为凸数(如120,363,374等),那么所有凸数个数为( )A.240 B.204 C.729 D.920
解析:可按十位数字进行分类;a2最小为2,最大为9,共分8类;
a2=2时,a1=1,a3=0,1
有两种;
a2=3时,a1可取1,2,a3可取0,1,2,共有2×3=6个
a2=4时,a1可取1,2,3,a3可取0,1,2,3,共3×4=12个
……
a2=9时,共有8×9=72个数,故所有凸数的个数为N=1×2+2×3+3×4+4×5+5×6+6×7+7×8+8×9 =240(个)
答案:A

练习册系列答案
相关题目
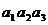 ”满足
”满足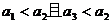 ,则称这样的三位数为凸数(如120、363、374等),那么所有凸数个数为_______________.(用数字作答)
,则称这样的三位数为凸数(如120、363、374等),那么所有凸数个数为_______________.(用数字作答)