题目内容
已知定圆C:x2+(y-3)2=4,过点A(-1,0)的一条动直线l与圆C相交于P,Q两点,若|PQ|=2
,则直线l的方程为( )
| 3 |
分析:根据题意画出图形,过C作CM垂直于PQ,根据垂径定理得到M为弦PQ的中点,求出|PM|的长,由圆的半径和|PM|,利用勾股定理求出|CM|,即为圆心C到直线l的距离,分两种情况:直线l的斜率不存在时,显然直线x=-1满足题意;当直线l斜率存在时,设出斜率为k,由直线l过A点,表示出直线l的方程,然后利用点到直线的距离公式表示出圆心到直线l的距离d,让d等于求出的|CM|列出关于k的方程,求出方程的解即可得到k的值,从而确定出直线l的方程,综上,得到所有满足题意的直线l的方程.
解答: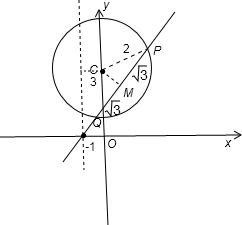 解:由题意画出图形,如图所示:
解:由题意画出图形,如图所示:
过圆心C作CM⊥PQ,则|MP|=|MQ|=
|PQ|=
,
由圆C的方程得到圆心C坐标(0,3),半径r=2,
在Rt△CPM中,根据勾股定理得:CM=1,即圆心到直线的距离为1,
(i)直线l的斜率不存在时,显然直线x=-1满足题意;
(ii)直线l的斜率存在时,设直线l的斜率为k,由A(-1,0),
得到直线l的方程为y=k(x+1),即kx-y+k=0,
圆心到直线l的距离d=
=1,解得k=
,
所以直线l为4x-3y+4=0,
综上,满足题意的直线l为x=-1或4x-3y+4=0.
故选C
 解:由题意画出图形,如图所示:
解:由题意画出图形,如图所示:过圆心C作CM⊥PQ,则|MP|=|MQ|=
| 1 |
| 2 |
| 3 |
由圆C的方程得到圆心C坐标(0,3),半径r=2,
在Rt△CPM中,根据勾股定理得:CM=1,即圆心到直线的距离为1,
(i)直线l的斜率不存在时,显然直线x=-1满足题意;
(ii)直线l的斜率存在时,设直线l的斜率为k,由A(-1,0),
得到直线l的方程为y=k(x+1),即kx-y+k=0,
圆心到直线l的距离d=
| |-3+k| | ||
|
| 4 |
| 3 |
所以直线l为4x-3y+4=0,
综上,满足题意的直线l为x=-1或4x-3y+4=0.
故选C
点评:此题考查了直线与圆的位置关系,利用了数形结合及分类讨论的思想,用到的知识有:垂径定理,勾股定理及点到直线的距离公式.若直线与圆相交时,常常利用弦长的一半,圆的半径及弦心距构造直角三角形解决问题.解本题时注意满足题意的直线l有两条,不要漏解.

练习册系列答案
相关题目
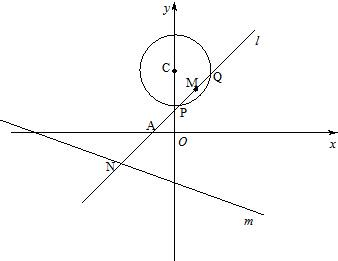 如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.
如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点. 如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.
如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点. 时,求直线l的方程;
时,求直线l的方程; ,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由.
,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由.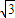 ,则直线l的方程为( )
,则直线l的方程为( ) 时,求直线l的方程;
时,求直线l的方程; ,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由.
,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由.