题目内容
如图,山顶有一座石塔BC,已知石塔的高度为a.
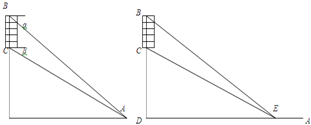
(Ⅰ)若以B,C为观测点,在塔顶B处测得地面上一点A的俯角为α,在塔底C处测得A处的俯角为β,用a,α,β表示山的高度h;
(Ⅱ)若将观测点选在地面的直线AD上,其中D是塔顶B在地面上的射影.已知石塔高度a=20,当观测点E在AD上满足DE=60
时看BC的视角(即∠BEC)最大,求山的高度h.

(Ⅰ)若以B,C为观测点,在塔顶B处测得地面上一点A的俯角为α,在塔底C处测得A处的俯角为β,用a,α,β表示山的高度h;
(Ⅱ)若将观测点选在地面的直线AD上,其中D是塔顶B在地面上的射影.已知石塔高度a=20,当观测点E在AD上满足DE=60
| 10 |
分析:(1)根据题意,在△ABC中算出∠BAC=α-β、∠BCA=90°+β,利用正弦定理加以计算,即可得到用a,α,β表示山的高度h的式子;
(2)设DE=x,利用正切的差角公式与三角函数的定义列式,然后根据基本不等式,可算出当x=
时,∠BEC最大,进而算出此时的h=180,即为所求山的高度.
(2)设DE=x,利用正切的差角公式与三角函数的定义列式,然后根据基本不等式,可算出当x=
| h(h+20) |
解答:解:(1)根据题意,可得
在△ABC中,∠BAC=α-β,∠BCA=90°+β,
由正弦定理,可得
=
∴AB=
=
则h=AB•sinα-a=
-a=
,即为所求表示式;
(2)设DE=x,
∵tan∠BED=
,tan∠CED=
∴tan∠BEC=
=
=
≤
当且仅当x=
即x=
时,tan∠BEC最大,从而∠BEC最大
结合题意,可得
=60
,解之得h=180,即为所求山的高度.
在△ABC中,∠BAC=α-β,∠BCA=90°+β,
由正弦定理,可得
| BC |
| sin∠BAC |
| AB |
| sin∠BCA |
∴AB=
| asin(90°+β) |
| sin(α-β) |
| acosβ |
| sin(α-β) |
则h=AB•sinα-a=
| acosβsinα |
| sin(α-β) |
| a•cosαsinβ |
| sin(α-β) |
(2)设DE=x,
∵tan∠BED=
| h+20 |
| x |
| h |
| x |
∴tan∠BEC=
| tan∠BED-tan∠CED |
| 1+tan∠BED•tan∠CED |
=
| ||
1+
|
| 20 | ||
x+
|
| 10 | ||
|
当且仅当x=
| (h+20)h |
| x |
| h(h+20) |
结合题意,可得
| h(h+20) |
| 10 |
点评:本题给出实际应用问题,求山高h的表示式并依此求视角最大时的山高h,着重考查了基本不等式、正弦定理与两角差正切公式等知识,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
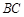 ,已知石塔的高度为
,已知石塔的高度为 .
.
 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 ,用
,用 表示山的高度
表示山的高度 ;
; 上,其中
上,其中 是塔顶
是塔顶 ,当观测点
,当观测点 在
在 时看
时看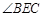 )最大,求山的高度
)最大,求山的高度