题目内容
设单调递增函数f(x)的定义域为(0,+∞),且对任意的正实数x,y有f(xy)=f(x)+f(y),且f(| 1 |
| 2 |
(1)一个各项均为正数的数列{an}满足:f(sn)=f(an)+f(an+1)-1其中Sn为数列{an}的前n项和,求数列{an}的通项公式;
(2)在(1)的条件下,是否存在正数M使下列不等式:2n•a1a2…an≥M
| 2n+1 |
分析:(1由题设知f(Sn)=f[(an2+an)×
].Sn=
(an2+an).由此能求出数列{an}的通项公式;
(2)、假设M≤
对一切n∈N*恒成立.令g(n)=
,g(n+1)=
.故
=
=
>1,由此能导出n∈N*,g(n)≥g(1)=
,0<M≤
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)、假设M≤
| 2na1a2an | ||
|
| 2na1a2an | ||
|
| 2n+1×1×2××n×(n+1) | ||
|
| g(n+1) |
| g(n) |
| 2n+2 | ||||
|
|
2
| ||
| 3 |
2
| ||
| 3 |
解答:解:(1)∵对任意的正数x、y均有f(xy)=f(x)+f(y)且f(
)=-1.(2分)
又∵an>0且f(Sn)=f(an)+f(an+1)-1=f(an)+f(an+1)+f(
).
∴f(Sn)=f[(an2+an)×
].(4分)
又∵f(x)是定义在(0,+∞]上的单增函数,
∴Sn=
(an2+an).
当n=1时,a1=
(a12+a1),
∴a12-a1=0∵a1>0,
∴a1=1.
当n≥2时,∵2an=2Sn-2Sn-1=an2+an-an-12-an-1,
∴(an+an-1)(an-an-1-1)=0.
∵an>0∴an-an-1=1(n≥2),
∴{an}为等差数列,a1=1,d=1
∴an=n.(6分)
(2)、假设M存在满足条件,即M≤
对一切n∈N*恒成立.(8分)
令g(n)=
,
∴g(n+1)=
.(10分)
故
=
=
>1,
∴g(n+1)>g(n),
∴g(n)单调递增,(12分)
∴n∈N*,g(n)≥g(1)=
,0<M≤
.(14分)
| 1 |
| 2 |
又∵an>0且f(Sn)=f(an)+f(an+1)-1=f(an)+f(an+1)+f(
| 1 |
| 2 |
∴f(Sn)=f[(an2+an)×
| 1 |
| 2 |
又∵f(x)是定义在(0,+∞]上的单增函数,
∴Sn=
| 1 |
| 2 |
当n=1时,a1=
| 1 |
| 2 |
∴a12-a1=0∵a1>0,
∴a1=1.
当n≥2时,∵2an=2Sn-2Sn-1=an2+an-an-12-an-1,
∴(an+an-1)(an-an-1-1)=0.
∵an>0∴an-an-1=1(n≥2),
∴{an}为等差数列,a1=1,d=1
∴an=n.(6分)
(2)、假设M存在满足条件,即M≤
| 2na1a2an | ||
|
令g(n)=
| 2na1a2an | ||
|
∴g(n+1)=
| 2n+1×1×2××n×(n+1) | ||
|
故
| g(n+1) |
| g(n) |
| 2n+2 | ||||
|
|
∴g(n+1)>g(n),
∴g(n)单调递增,(12分)
∴n∈N*,g(n)≥g(1)=
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查数列的性质和应用,解题时要认真审题,注意公式的合理运用.

练习册系列答案
相关题目
 .
.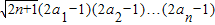 对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.
对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.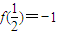 .
.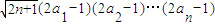 对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.
对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.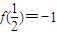 .
.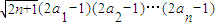 对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.
对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.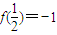 .
.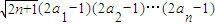 对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.
对一切n∈N*成立?若存在,求出M的取值范围;若不存在,请说明理由.