题目内容
已知全集U=R集合A={x|x2-x-6<0},B={x|x2+2x-8>0},C={x|x2-4ax+3a2<0},若?U(A∪B)⊆C,则实数a的取值范围是
(-2,-
)
| 4 |
| 3 |
(-2,-
)
.| 4 |
| 3 |
分析:求出A与B中不等式的解集,确定出A与B,求出A与B的并集,找出并集的补集,分a等于0,大于0及小于0三种情况分别表示出集合C中不等式的解集,根据补集为C的子集列出关于a的不等式,求出不等式的解集即可确定出a的范围.
解答:解:集合A={x|x2-x-6<0}={x|-2<x<3},B={x|x2+2x-8>0}={x|x>2或x<-4},
∴A∪B={x|x>-2或x<-4},
∵全集为U=R,∴?U(A∪B)={x|-4≤x≤-2},
分三种情况考虑:
①当a=0时,集合C=∅,?U(A∪B)⊆C不成立,舍去;
②当a>0时,集合C={x|a<x<3a},?U(A∪B)⊆C不成立,舍去;
③当a<0时,集合C={x|3a<x<a},要使?U(A∪B)⊆C成立,则有
,
解得:-2<a<-
,
综上实数a的范围是(-2,-
).
故答案为:(-2,-
)
∴A∪B={x|x>-2或x<-4},
∵全集为U=R,∴?U(A∪B)={x|-4≤x≤-2},
分三种情况考虑:
①当a=0时,集合C=∅,?U(A∪B)⊆C不成立,舍去;
②当a>0时,集合C={x|a<x<3a},?U(A∪B)⊆C不成立,舍去;
③当a<0时,集合C={x|3a<x<a},要使?U(A∪B)⊆C成立,则有
|
解得:-2<a<-
| 4 |
| 3 |
综上实数a的范围是(-2,-
| 4 |
| 3 |
故答案为:(-2,-
| 4 |
| 3 |
点评:此题考查了交、并、补集的混合运算,以及集合间的包含关系判断及应用,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目

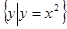 ,集合B=
,集合B= ,则
,则 为( )。
为( )。 B.R C.
B.R C. D.
D.
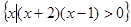 ,B=
,B= 则A
则A (CUB)
(CUB)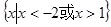 B.
B.
 D.
D.