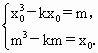题目内容
| |||||||||||
解析:
(1) |
解析:∵a=( 又∵x⊥y,∴x·y=0, ∴[a+(t2-k)b]·(sa+tb)=0, ∴-sa2+(t-k)tb2+(t-st2+sk)a·b=0,∴s=t3-kt,即s=f(t)=t3-kt. |
(2) |
① 又∵f(t)是单调函数,∴若f(t)是增函数。则f'(t)≥0.恒有3t2≥k,而t∈[1,+∞],∴0<k≤3. 若f(t)是减函数,则f'(t)≤0,恒有3t2≤k,而t∈[1,+∞]、这样的k不存在,∴0<k≤3. ②方法一 设f(x0)=m,由f[(x0)]=x0, 得f(m)=x0,∴ 两式相减,有( ∴(x0-m)( ∵x0≥1,m=f(x0)≥1, ∴ 而0<k≤3,∴ ∴x0-m=0,∴x0=m,∴f(x0)=x0. 方法二 若f(x0)>x0≥1,∵f(t)在[1,+∞)上是单调增函数。∴f(f(x0))>f(x0)>x0. 与f(f(x0))=x0矛盾. 若1≤f(x0)<x0,∵f(t)在[1,+∞]上是单调增函数,∴f(f(x0))<f(x0)<x0. 与f(f(x0))=x0矛盾,∴f(x0)=x0. 点评:本题主要考查:(1)平面向量数量积的运算;(2)导数的性质;(3)恒成立的不等式字母参数取值范围的求法;(4)关于不动点的证明问题.本题是一道综合性较强的试题,覆盖了中学数学中的重要知识,体现了在知识网络交汇点设计试题的高考命题思想. |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案