题目内容
【例】
已知函数y=sin2x+![]() cos2x-2.
cos2x-2.
(1)用“五点法”作出函数在一个周期内的图象;
(2)求这个函数的周期和单调区间;
(3)求函数图象的对称轴方程.
(4)说明图象是由y=sinx的图象经过怎样的变换得到的.
![]() 学科网
学科网
T=![]() =π,单调增区间为[-
=π,单调增区间为[-![]() π+kπ
π+kπ![]() +kπ],k∈Z;,函数的单调减区间为[
+kπ],k∈Z;,函数的单调减区间为[![]() +kπ,
+kπ,![]() π+kπ],k∈Z
π+kπ],k∈Z
解析:
解: y=sin2x+![]() cos2x-2=2sin(2x+
cos2x-2=2sin(2x+![]() )-2.
)-2.
(1)列表
| x | - |
|
|
|
|
| 2x+ | 0 |
| π |
| 2π |
| y=2sin(2x+ | -2 | 0 | -2 | -4 | -2 |
其图象如下图所示.
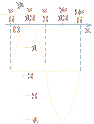
(2)T=![]() =π.
=π.
由-![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ,知函数的单调增区间为[-
+2kπ,知函数的单调增区间为[-![]() π+kπ
π+kπ![]() +kπ],k∈Z;
+kπ],k∈Z;
由![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() π+2kπ,知函数的单调减区间为[
π+2kπ,知函数的单调减区间为[![]() +kπ,
+kπ,![]() π+kπ],k∈Z.
π+kπ],k∈Z.
(3)由2x+![]() =
=![]() +kπ得x=
+kπ得x=![]() +
+![]() π.
π.
∴函数图象的对称轴方程为x=![]() +
+![]() π(k∈Z).
π(k∈Z).
(4)把函数y1=sinx的图象上所有的点向左平移![]() 个单位,得到函数y2=sin(x+
个单位,得到函数y2=sin(x+![]() )的图象;
)的图象;
再把y2图象上各点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到y3=sin(2x+
倍(纵坐标不变),得到y3=sin(2x+![]() )的图象;
)的图象;
再把y3图象上各点的纵坐标伸长到原来的2倍(横坐标不变),得到y4=2sin(2x+![]() )的图象;
)的图象;
最后把y4图象上所有的点向下平移2个单位,得到函数y=2sin(2x+![]() )-2的图象.
)-2的图象.
评注:(1)求函数的周期、单调区间、最值等问题,一般都要化成一个角的三角函数形式.
(2)对于函数y=Asin(ωx+![]() )的对称轴,实际上就是使函数y取得最大值或最小值时的x值.
)的对称轴,实际上就是使函数y取得最大值或最小值时的x值.
(3)第(4)问的变换方法不唯一,但必须特别注意平移变换与伸缩变换的先后顺序.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目