题目内容
设x1,x2是方程ln|x-2|=m(m为实常数)的两根,则x1+x2的值为( )
分析:由已知中x1,x2是方程ln|x-2|=m(m为实常数)的两根,根据函数y=ln|x-2|-m的图象关于直线x=2对称,可得答案.
解答:解:令函数y=ln|x-2|-m,则函数的图象关于直线x=2对称
若x1,x2是方程ln|x-2|=m(m为实常数)的两根,
则x1,x2是函数y=ln|x-2|-m的两个零点,
其值必关于直线x=2对称
则x1+x2=4
故选A
若x1,x2是方程ln|x-2|=m(m为实常数)的两根,
则x1,x2是函数y=ln|x-2|-m的两个零点,
其值必关于直线x=2对称
则x1+x2=4
故选A
点评:本题考查的知识点是对数函数的图象与性质的综合应用,其中分析出函数y=ln|x-2|-m的图象关于直线x=2对称是解答本题的关键.

练习册系列答案
相关题目
 x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}. ;
;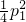 ),E′(p2,
),E′(p2,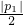 .
. }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax) x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}. p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=
p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)= ;
; ),E′(p2,
),E′(p2, p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=
p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)= .
. (x+1)2-
(x+1)2- }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax) x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}. p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=
p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)= ;
; ),E′(p2,
),E′(p2, p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=
p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=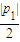 .
. (x+1)2-
(x+1)2- }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)