题目内容
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|<1)上一点M的切线l,与曲线C2:y= (|x|<1)也相切于点N,记点M的横坐标为t(t>1)。
(|x|<1)也相切于点N,记点M的横坐标为t(t>1)。
(1)用t表示m的值和点N的坐标;
(2)当实数m取何值时,∠MAB=∠NAB?并求此时MN所在直线的方程。
 (|x|<1)也相切于点N,记点M的横坐标为t(t>1)。
(|x|<1)也相切于点N,记点M的横坐标为t(t>1)。(1)用t表示m的值和点N的坐标;
(2)当实数m取何值时,∠MAB=∠NAB?并求此时MN所在直线的方程。

解:(1)切线 ,即
,即 ,
,
代入 ,
,
化简并整理得, (*),
(*),
由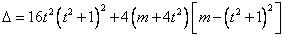
 ,
,
得m=0或 。
。
若m=0,代入(*)式得 ,与已知
,与已知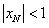 矛盾;
矛盾;
若 ,代入(*)式得,
,代入(*)式得,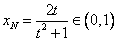 满足条件,
满足条件,
且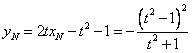 ;
;
综上, ,点N的坐标为
,点N的坐标为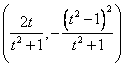 。
。
(2)因为, ,
, ,
,
若∠MAB=∠NAB,则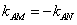 ,即t=2,此时m=9,
,即t=2,此时m=9,
故当实数m=9时,∠MAB=∠NAB,
此时,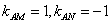 ,∠MAB=∠NAB=45°,
,∠MAB=∠NAB=45°,
易得M(2,3),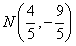 ,
,
所以,此时MN所在直线的方程为y=4x-5。
 ,即
,即 ,
,代入
 ,
,化简并整理得,
 (*),
(*),由
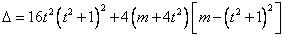
 ,
,得m=0或
 。
。若m=0,代入(*)式得
 ,与已知
,与已知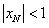 矛盾;
矛盾;若
 ,代入(*)式得,
,代入(*)式得,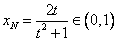 满足条件,
满足条件,且
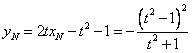 ;
;综上,
 ,点N的坐标为
,点N的坐标为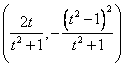 。
。(2)因为,
 ,
, ,
,若∠MAB=∠NAB,则
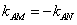 ,即t=2,此时m=9,
,即t=2,此时m=9,故当实数m=9时,∠MAB=∠NAB,
此时,
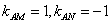 ,∠MAB=∠NAB=45°,
,∠MAB=∠NAB=45°,易得M(2,3),
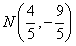 ,
,所以,此时MN所在直线的方程为y=4x-5。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
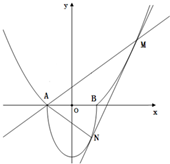 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线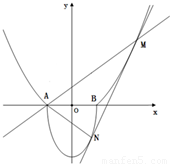 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线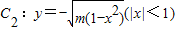 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).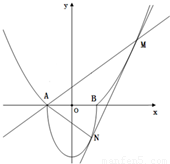 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线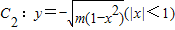 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).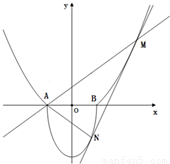 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线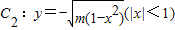 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).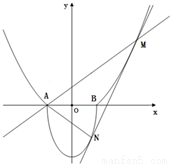 如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线 也相切于点N,记点M的横坐标为t(t>1).
也相切于点N,记点M的横坐标为t(t>1).