题目内容
一项试验有两套方案,每套方案试验成功的概率都是| 2 |
| 3 |
| 1 |
| 3 |
(I)求3次试验都选择了同一套方案且都试验成功的概率;
(II)3次试验中,都选择了第-套方案且至少成功1次的概率.
分析:(I)由已知中每套方案试验成功的概率都是
,试验不成功的概率都是
.我们易计算出一次试验中,选择第i套方案并试验成功的概率,则3次试验都选择了同一套方案且都试验成功,包括两种情形,一是均选第一套方案,二是均选第二套方案,代入互斥事件概率加法公式,即可得到答案.
(II)结合(I)的结论,我们易求出三次试验均不成功的概率,然后代入对立事件概率减法公式,即可得到答案.
| 2 |
| 3 |
| 1 |
| 3 |
(II)结合(I)的结论,我们易求出三次试验均不成功的概率,然后代入对立事件概率减法公式,即可得到答案.
解答:解:记事件“一次试验中,选择第i套方案并试验成功”为Ai,i=1,2,则
P(Ai)=
×
=
.
(Ⅰ)3次试验选择了同一套方案且都试验成功的概率
P=P(A1•A1•A1+A2•A2•A2)=(
)3+(
)3=
.
(Ⅱ)3次试验中,都选择第一套方案并至少试验成功1次的概率
P′=1-(
)3=
.
P(Ai)=
| 1 | ||
|
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ)3次试验选择了同一套方案且都试验成功的概率
P=P(A1•A1•A1+A2•A2•A2)=(
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
(Ⅱ)3次试验中,都选择第一套方案并至少试验成功1次的概率
P′=1-(
| 2 |
| 3 |
| 19 |
| 27 |
点评:本题考查的知识点是相互独立事件的概率乘法公式,互斥事件概率加法公式,对立事件概率减法公式,其中分析事件与事件之间的关系,从而选择恰当的公式进行解答,是处理本题的关键.

练习册系列答案
相关题目
 ,试验不成功的概率都是
,试验不成功的概率都是 甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套. ,试验不成功的概率都是
,试验不成功的概率都是 甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.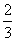 ,试验不成功的概率都是
,试验不成功的概率都是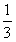 ,甲随机地从两套方案中选取一套进行这项试验,共试验了3次,每次试验相互独立,且要从两套方案中等可能地选择一套。(1)求3次试验都选择了同一套方案且都试验成功的概率;
,甲随机地从两套方案中选取一套进行这项试验,共试验了3次,每次试验相互独立,且要从两套方案中等可能地选择一套。(1)求3次试验都选择了同一套方案且都试验成功的概率;