题目内容
已知方程
是关于
的一元二次方程．
（1）若
是从集合
四个数中任取的一个数，
是从集合
三个数中任取的一个数，求上述方程有实数根的概率；
（2）若
，
，求上述方程有实数根的概率．
是关于的一元二次方程．（1）若
是从集合四个数中任取的一个数，是从集合三个数中任取的一个数，求上述方程有实数根的概率；（2）若
，，求上述方程有实数根的概率．（1）
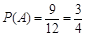（2）
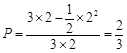
试题分析：（1）先将从集合
四个数中任取的一个数作为，从集合三个数中任取的一个数作为的所有情况列出来，再将使上述方程由实数根的情况列出来，根据古典概型公式算出所求事件的概率；（2）先作出满足，表示的平面区域并计算出区域的面积S，再根据要使方程有实数根，则△≥0，求出a,b满足的不等式，作出该不等式与，表示区域并计算面积，根据几何概型公式，该面积与S的比值就是上述方程有实数根的概率.试题解析：设事件
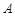为“方程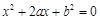
有实数根”．当
，
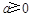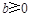时，方程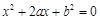有实数根的充要条件为
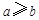．（1）基本事件共12个：
，
，
，
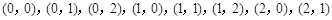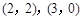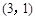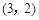．其中第一个数表示
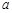的取值，第二个数表示
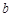的取值．事件
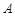中包含9个基本事件．事件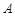发生的概率为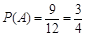．（2）试验的全部结果所构成的区域为
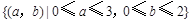．构成事件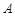的区域为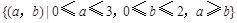
．所以所求的概率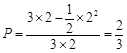．考点:古典概型；几何概型
练习册系列答案
相关题目
第2组
第3组
第4组
第5组
得到的频率分布直方图如图所示,
分别表示英语成绩和数学成绩的等级分（例如表中英语成绩等级分为5分的共6人，数学成绩等级分为3分的共15人）．由已知表格，试填写出对应的表格（见答题卷中的表格）．也即求出下列各对应值：
的概率P
的概率P
的概率P
的概率P（E）及对应的
的值．
