题目内容
函数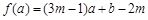 ,当
,当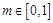 时,
时,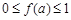 恒成立,则
恒成立,则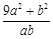 的最大值与最小值之和为( )
的最大值与最小值之和为( )
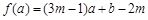 ,当
,当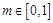 时,
时,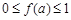 恒成立,则
恒成立,则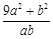 的最大值与最小值之和为( )
的最大值与最小值之和为( )| A.18 | B.16 | C.14 | D.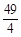 |
B
试题分析:令
 ,因为当
,因为当 时,
时, 恒成立,即
恒成立,即 恒成立,所以
恒成立,所以 ,即
,即
满足上述条件的点
 的可行域如下:
的可行域如下: 
由图可知,目标函数
 在边界
在边界 上取到最小值1,在点
上取到最小值1,在点 处取到最大值4,所以
处取到最大值4,所以
而
 ,令
,令 ,则
,则
 ,
, ,当
,当 时,
时, ,此时函数
,此时函数 单调递减,当
单调递减,当 时,
时, ,此时函数
,此时函数 单调递增
单调递增所以函数
 在点
在点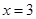 处取到最小值6,因为
处取到最小值6,因为 时
时 ,
, 时
时
所以函数
 在点
在点 处取到最大值10
处取到最大值10 所以
 的最小值为6,最大值为10,则两者之和为16,故选B
的最小值为6,最大值为10,则两者之和为16,故选B 
练习册系列答案
相关题目
 满足不等式组
满足不等式组 ,则目标函数
,则目标函数 的最大值为_________.
的最大值为_________.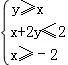 ,则z=x﹣3y的最小值( )
,则z=x﹣3y的最小值( ) (其中
(其中 )表示的平面区域的面积为4,点
)表示的平面区域的面积为4,点 在该平面区域内,则
在该平面区域内,则 的最大值为( )
的最大值为( ) ,
, 满足条件
满足条件 则
则 的最大值为 .
的最大值为 . 满足
满足 ,则
,则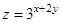 的值域是( )
的值域是( )



 是定义在
是定义在 上的增函数,且对于任意的
上的增函数,且对于任意的 都有
都有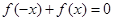 恒成立.如果实数
恒成立.如果实数 满足不等式
满足不等式 ,那么
,那么 的取值范围是
的取值范围是
 满足约束条件
满足约束条件 则
则 的最小值为 。
的最小值为 。 则该约束条件所围成的平面区域的面积是( )
则该约束条件所围成的平面区域的面积是( )
