题目内容
【题目】在教材中,我们已研究出如下结论:平面内![]() 条直线最多可将平面分成
条直线最多可将平面分成![]() 个部分.现探究:空间内
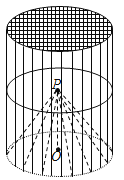
个部分.现探究:空间内![]() 个平面最多可将空间分成多少个部分,
个平面最多可将空间分成多少个部分,![]() .设空间内
.设空间内![]() 个平面最多可将空间分成
个平面最多可将空间分成![]() 个部分.
个部分.
(1)求![]() 的值;
的值;
(2)用数学归纳法证明此结论.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)将![]() 代入
代入![]() 得到方程组,求解得到结果;(2)根据数学归纳法的步骤,当
得到方程组,求解得到结果;(2)根据数学归纳法的步骤,当![]() 时,利用
时,利用![]() 整理出结论.
整理出结论.
(1)由![]() 得
得
解得![]()
(2)用数学归纳法证明![]()
①当![]() 时,显然成立
时,显然成立
②假设当![]() 时成立,即
时成立,即![]()
那么当![]() 时,在
时,在![]() 个平面的基础上再添上第
个平面的基础上再添上第![]() 个平面
个平面
因为它和前![]() 个平面都相交,所以可得到
个平面都相交,所以可得到![]() 条互不平行且不共点的交线,且其中任何
条互不平行且不共点的交线,且其中任何![]() 条直线不共点,这
条直线不共点,这![]() 条交线可以把第
条交线可以把第![]() 个平面划分成
个平面划分成![]() 个部分;每个部分把它所在的原有空间区域划分成两个区域,因此,空间区域的总数增加了
个部分;每个部分把它所在的原有空间区域划分成两个区域,因此,空间区域的总数增加了![]() 个,所以
个,所以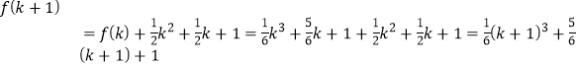 即
即![]() 时,结论成立
时,结论成立
根据①②可知,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目