Question

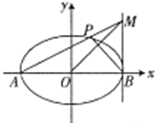如图所示，平面直角坐标系中，已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0），A、B是其左、右顶点，动点M满足MB⊥AB，连接AM交椭圆于点P，若MO⊥PB，则椭圆的离心率为

2

2

．

Answer 1

分析：可设出直线AM的方程，与直线MB的方程联立可求得M点的坐标，从而可得OM的斜率，继而有直线BP的方程，与直线AM的方程联立可求得P点的坐标，代入椭圆方程，整理即可求得椭圆的离心率．

解答：解：依题意，A（-a，0），设直线AM的方程为：y=k（x+a），①与直线MB的方程联立得M（a，2ka），
∴OM的斜率k_OM=2k，
∵MO⊥PB，
∴k_BP=-

1

2k

，又B（a，0），
∴直线BP的方程为：y=-

1

2k

（x-a），②
∴由①②联立

y=k(x+a) y=- 1 2k (x-a)

得P点的坐标为：P（

a(1-2k2)

2k2+1

，

2ak

2k2+1

），
∵点P在椭圆

x2

a2

+

y2

b2

=1（a＞b＞0），
∴

( a(1-2k2) 2k2+1 )2

a2

+

( 2ak 2k2+1 )2

b2

=1，
∴4a²k²=8b²k²，k≠0，
∴a²=2b²=2（a²-c²），
∴a²=2c²，
∴e=

c

a

=

2

2

．
故答案为：

2

2

．

点评：本题考查直线的方程，考查直线的垂直，考查椭圆的方程与椭圆的性质的综合应用，求得P点的坐标是关键，也是难点，考查抽象思维与推理运算能力，属于难题．