题目内容
据相关调查数据统计,2010年某大城市私家车平均每天增加400辆,除此之外,公交车等公共车辆也增长过快,造成交通拥堵现象日益严重,现有A、B、C三辆车从同一地点同时出发,开往甲、乙、丙三地,已知A、B、C这三辆车在驶往目的地的过程中,出现堵车的概率依次为
,
,
,且每辆车是否被堵互不影响.
(1)求这三辆车恰有两辆车被堵的概率;
(2)求这三辆车至少有两辆车不被堵的概率.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
(1)求这三辆车恰有两辆车被堵的概率;
(2)求这三辆车至少有两辆车不被堵的概率.
分析:由对立事件的概率结合题意可得:(1)所求概率为
×
×(1-
)+(1-
)×
×
+
×(1-
)×
,计算可得;
(2)这三辆车至少有两辆车不被堵,即恰有2辆不堵,或3辆都不堵,分别求得相加即可.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
(2)这三辆车至少有两辆车不被堵,即恰有2辆不堵,或3辆都不堵,分别求得相加即可.
解答:解:(1)由题意可得这三辆车恰有两辆车被堵的概率为:
×
×(1-
)+(1-
)×
×
+
×(1-
)×
=
(2)这三辆车至少有两辆车不被堵,即恰有2辆不堵,或3辆都不堵,
其中3辆都不堵概率为:
×
×
=
,
恰有2辆不堵的概率为:
×
×
+
×
×
+
×
×
=
故所求概率为:
+
=
=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 32 |
(2)这三辆车至少有两辆车不被堵,即恰有2辆不堵,或3辆都不堵,
其中3辆都不堵概率为:
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 9 |
| 32 |
恰有2辆不堵的概率为:
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 15 |
| 32 |
故所求概率为:
| 9 |
| 32 |
| 15 |
| 32 |
| 24 |
| 32 |
| 3 |
| 4 |
点评:本题考查古典概型的计算公式及相互独立事件的概率公式,理清事件与事件之间的关系是解决问题的关键,属基础题.

练习册系列答案
相关题目
 ,且每辆车是否被堵互不影响.
,且每辆车是否被堵互不影响. ,且每辆车是否被堵互不影响.
,且每辆车是否被堵互不影响.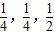 ,且每辆车是否被堵互不影响.
,且每辆车是否被堵互不影响.