题目内容
有一种单细胞以一分为二的方式繁殖,每3分钟分裂一次,假设将一个这种细胞放在一个盛有营养液的容器中,恰好一小时后这种细胞充满容器,假如开始时将两个这种细胞放入该容器,同样充满容器的时间是( )A.27分钟
B.30分钟
C.45分钟
D.57分钟
【答案】分析:一小时共计60分钟,该细胞每3分钟分裂一次,共分裂20次,则细胞每次分裂后得到的新细胞构成了以2为首项,以2为公比的等比数列,一小时后的数列个数为a20;若开始时放入的是两个单细胞,则3分钟后为4个,细胞每次分裂后得到的新细胞构成了以4为首项,以2为公比的等比数列,有了充满容器时的细胞总数,求项数.
解答:解:设a1=2,公比q=2,则 .
.
再设b1=4,公比q=2,由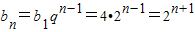 ,
,
由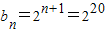 ,得n=19,
,得n=19,
即细胞要分裂19次才能充满容器,所以分裂时间为19×3=57分钟.
故选D.
点评:本题考查了等比数列的通项公式,解答的关键是两个等比数列的项相等,求第二个数列的项数,属基础题.
解答:解:设a1=2,公比q=2,则
 .
.再设b1=4,公比q=2,由
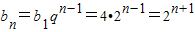 ,
,由
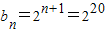 ,得n=19,
,得n=19,即细胞要分裂19次才能充满容器,所以分裂时间为19×3=57分钟.
故选D.
点评:本题考查了等比数列的通项公式,解答的关键是两个等比数列的项相等,求第二个数列的项数,属基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目