题目内容
(本小题满分12分)
过点P(1,4)作直线L,直线L与x,y的正半轴分别交于A,B两点,O为原点,
①△ABO的面积为S,求S的最小值并求此时直线l的方程;
②当|OA|+|OB|最小时,求此时直线L的方程
过点P(1,4)作直线L,直线L与x,y的正半轴分别交于A,B两点,O为原点,
①△ABO的面积为S,求S的最小值并求此时直线l的方程;
②当|OA|+|OB|最小时,求此时直线L的方程
解:依题意可设直线l的方程为: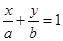 (a>0 , b>0 )
(a>0 , b>0 )
则A(a , 0 ), B(0,b ), 直线L过点P(1,4), ∴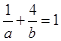 , ……………2分
, ……………2分
又a>0 , b>0
∴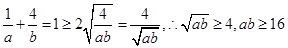
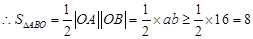 ………………4分
………………4分
当且仅当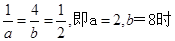 取等号, S的最小值为8
取等号, S的最小值为8
此时直线方程为: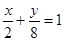 ,即:4x + y - 8=0…………………6分
,即:4x + y - 8=0…………………6分
②|OA|+|OB|=" a" + b =" (a" + b )( )="5" +
)="5" + 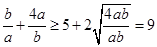 ……8分
……8分
当且仅当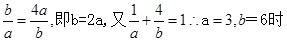 取等号, ……10分
取等号, ……10分
|OA|+|OB|的值最小, 此时直线方程为: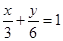 即:2x + y - 6=0……12分
即:2x + y - 6=0……12分
法二:①依题意可设直线l的方程为:y-4 =" k" ( x -1 ) ( k<0 )
令 x =" 0" , 则y =" 4" – k ,B( 0 , 4-k) ;令 y =" 0" , 则x =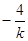 +1 ,A (
+1 ,A (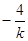 +1, 0)…2分
+1, 0)…2分
S =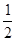 (4-k)(
(4-k)( 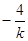 +1)=
+1)= 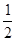 (
( - k + 8 )≥8 ,…………4分
- k + 8 )≥8 ,…………4分
当且仅当-16/k = -k时,即 k = -4时取等号, S的最小值为8 ,
此时直线方程为:y-4 =" -4(" x -1 ),即:4x + y - 8=0…………6分
②|OA|+|OB|="("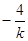 +1) + (4-k) =
+1) + (4-k) = 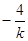 -k + 5 ≥4 + 5 ="9" ,……8分
-k + 5 ≥4 + 5 ="9" ,……8分
当且仅当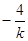 = -k时,即 k = -2时取等号, |OA|+|OB|的值最小, ……………10分
= -k时,即 k = -2时取等号, |OA|+|OB|的值最小, ……………10分
此时直线方程为::y-4 =" -2" ( x -1 ) 即:2x + y - 6=0……………12分
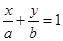 (a>0 , b>0 )
(a>0 , b>0 )则A(a , 0 ), B(0,b ), 直线L过点P(1,4), ∴
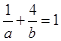 , ……………2分
, ……………2分又a>0 , b>0
∴
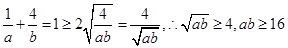
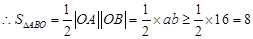 ………………4分
………………4分当且仅当
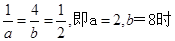 取等号, S的最小值为8
取等号, S的最小值为8此时直线方程为:
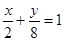 ,即:4x + y - 8=0…………………6分
,即:4x + y - 8=0…………………6分②|OA|+|OB|=" a" + b =" (a" + b )(
 )="5" +
)="5" + 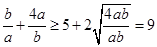 ……8分
……8分当且仅当
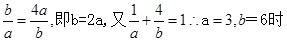 取等号, ……10分
取等号, ……10分|OA|+|OB|的值最小, 此时直线方程为:
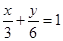 即:2x + y - 6=0……12分
即:2x + y - 6=0……12分法二:①依题意可设直线l的方程为:y-4 =" k" ( x -1 ) ( k<0 )
令 x =" 0" , 则y =" 4" – k ,B( 0 , 4-k) ;令 y =" 0" , 则x =
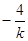 +1 ,A (
+1 ,A (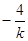 +1, 0)…2分
+1, 0)…2分S =
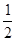 (4-k)(
(4-k)( 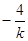 +1)=
+1)= 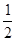 (
( - k + 8 )≥8 ,…………4分
- k + 8 )≥8 ,…………4分当且仅当-16/k = -k时,即 k = -4时取等号, S的最小值为8 ,
此时直线方程为:y-4 =" -4(" x -1 ),即:4x + y - 8=0…………6分
②|OA|+|OB|="("
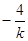 +1) + (4-k) =
+1) + (4-k) = 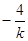 -k + 5 ≥4 + 5 ="9" ,……8分
-k + 5 ≥4 + 5 ="9" ,……8分当且仅当
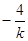 = -k时,即 k = -2时取等号, |OA|+|OB|的值最小, ……………10分
= -k时,即 k = -2时取等号, |OA|+|OB|的值最小, ……………10分此时直线方程为::y-4 =" -2" ( x -1 ) 即:2x + y - 6=0……………12分
略

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
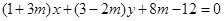
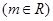 与圆
与圆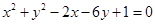 的交点个数为( )
的交点个数为( )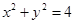 上,与直线
上,与直线 的距离最小的点的坐标为( )
的距离最小的点的坐标为( )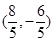



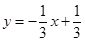
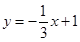
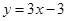
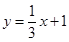
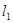 在
在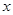 轴和
轴和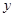 轴上的截距分别为
轴上的截距分别为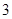 和
和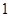 ,直线
,直线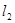 的方程为
的方程为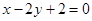 ,则直线
,则直线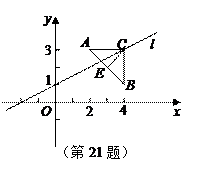
 满足
满足 , 则直线
, 则直线 过定点 ( ▲ )
过定点 ( ▲ )


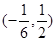
 和直线
和直线 具有相同的法向量.则
具有相同的法向量.则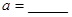
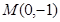 ,点
,点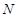 在直线
在直线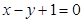 上,若直线
上,若直线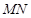 垂直于直线
垂直于直线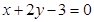 , 则点
, 则点