题目内容
如果圆x2+y2=k2至少覆盖函数f(x)=
sin
的一个极大值点和一个极小值点,则k的取值范围是
| 3 |
| πx |
| k |
(-∞,-2]∪[2,+∞)
(-∞,-2]∪[2,+∞)
.分析:根据题意可得函数离原点最近一个极大值点(
,
)在圆x2+y2=k2内或在圆上,即
+3≤k2,解此不等式求得
k的取值范围.
| k |
| 2 |
| 3 |
| k2 |
| 4 |
k的取值范围.
解答:解:f(x)=
sin
的离原点最近一个极大值点(
,
)在圆x2+y2=k2内或在圆上,∴
+3≤k2,
解得 k≥2,或 k≤-2,
故答案为:(-∞,-2]∪[2,+∞).
| 3 |
| πx |
| k |
| k |
| 2 |
| 3 |
| k2 |
| 4 |
解得 k≥2,或 k≤-2,
故答案为:(-∞,-2]∪[2,+∞).
点评:本题考查点与圆的位置关系,三角函数的最值,得到
+3≤k2,是解题的关键.
| k2 |
| 4 |

练习册系列答案
相关题目
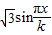 的一个极大值点和一个极小值点,则k的取值范围是 .
的一个极大值点和一个极小值点,则k的取值范围是 .