题目内容
我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(-3,4),且法向量为 =(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系o-xyz中,经过点A(1,2,3)且法向量为
=(1,-2)的直线(点法式)方程为:1×(x+3)+(-2)×(y-4)=0,化简得x-2y+11=0.类比以上方法,在空间直角坐标系o-xyz中,经过点A(1,2,3)且法向量为 =(-1,-2,1)的平面的方程为____________ .
=(-1,-2,1)的平面的方程为____________ .
(化简后用关于x,y,z的一般式方程表示)
【答案】
x+2y-z-2=0
【解析】
试题分析:根据法向量的定义,若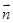 为平面α的法向量,则
为平面α的法向量,则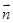 ⊥α,任取平面α内一点P(x,y,z),
⊥α,任取平面α内一点P(x,y,z),
则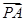 ⊥
⊥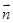 ,∵
,∵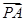 =(1-x,2-y,3-z),
=(1-x,2-y,3-z),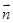 =(-1,-2,1),∴(x-1)+2(y-2)+(3-z)=0,即x+2y-z-2=0,
=(-1,-2,1),∴(x-1)+2(y-2)+(3-z)=0,即x+2y-z-2=0,
故答案为x+2y-z-2=0。
考点:本题主要考查类比推理的概念和方法,向量的坐标运算。
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).由于平面向量与空间向量的坐标运算类似,因此可以利用求平面曲线方程的办法,通过构造向量,利用向量的运算确定空间平面方程。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的直线(点法式)方程为
的直线(点法式)方程为 类比以上方法,在空间直角坐标系中,经过点A(1,2,3)且法向量为
类比以上方法,在空间直角坐标系中,经过点A(1,2,3)且法向量为 的平面(点法式)方程为 。(请写出化简后的结果)
的平面(点法式)方程为 。(请写出化简后的结果)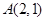 且法向量
且法向量 的直线(点法式)方程为
的直线(点法式)方程为 化简后得
化简后得 ;类比以上求法,在空间直角坐标系中,经过点
;类比以上求法,在空间直角坐标系中,经过点 且法向量为
且法向量为 的平面(点法式)方程为
的平面(点法式)方程为  (请写出化简后的结果).
(请写出化简后的结果). ,且法向量为
,且法向量为 的直线(点法式)方程为
的直线(点法式)方程为 ,化简得
,化简得 . 类比以上方法,在空间直角坐标系中,经过点
. 类比以上方法,在空间直角坐标系中,经过点 ,且法向量为
,且法向量为 的平面(点法式)方程为
的平面(点法式)方程为