题目内容
已知对于自然数a，存在一个以a为首项系数的整系数二次三项式，它有两个小于1的正根，求证：a≥5．
证明：设二次三项式为：f（x）=a（x-x1）（x-x2），a∈N．
依题意知：0＜x1＜1，0＜x2＜1，且x1≠x2．于是有
f（0）＞0，f（1）＞0．
又f（x）=ax2-a（x1+x2）x+ax1x2为整系数二次三项式，
所以f（0）=ax1x2，f（1）=a•（1-x1）（1-x2）为正整数
故f（0）≥1，f（1）≥1．
从而f（0）•f（1）≥1．①
另一方面，
x1（1-x1）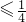
，x2（1-x2）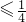
且由x1≠x2知等号不同时成立，所以
x1（1-x1）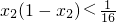
a2x1（1-x1）x2（1-x2）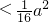
由①、②得，a2＞16．又a∈N，所以a≥5．
分析：设出二次函数的零点式，抓住整系数多项式，各系数都是整数，结合f（0）≥1，f（1）≥1，利用不等式化简变形即可．
点评：本题考查二次函数的证明问题以及不等式的简单应用，关键是灵活运用“整数系数”限制范围，属于中档题．
依题意知：0＜x1＜1，0＜x2＜1，且x1≠x2．于是有
f（0）＞0，f（1）＞0．
又f（x）=ax2-a（x1+x2）x+ax1x2为整系数二次三项式，
所以f（0）=ax1x2，f（1）=a•（1-x1）（1-x2）为正整数
故f（0）≥1，f（1）≥1．
从而f（0）•f（1）≥1．①
另一方面，
x1（1-x1）
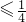，x2（1-x2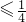）且由x1≠x2知等号不同时成立，所以
x1（1-x1）
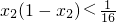
a2x1（1-x1）x2（1-x2）
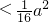
由①、②得，a2＞16．又a∈N，所以a≥5．
分析：设出二次函数的零点式，抓住整系数多项式，各系数都是整数，结合f（0）≥1，f（1）≥1，利用不等式化简变形即可．
点评：本题考查二次函数的证明问题以及不等式的简单应用，关键是灵活运用“整数系数”限制范围，属于中档题．
练习册系列答案
相关题目