题目内容
附加题:(二选一,请将解题过程解答在相应的框内,答错位置不给分;多答按第一问给分,不重复给分)
(1)已知a,b,c>0,且a2+b2=c2,求证:an+bn<cn(n≥3,n∈R+)
(2)已知x,y,z>0,则
+
>
.
(1)已知a,b,c>0,且a2+b2=c2,求证:an+bn<cn(n≥3,n∈R+)
(2)已知x,y,z>0,则
| x2+y2+xy |
| y2+z2+yz |
| z2+x2+xz |
分析:(1)利用指数函数y=ax当0<a<1时单调递减即可证明;
(2)利用余弦定理和三角形的两边之和大于第三边即可证明.
(2)利用余弦定理和三角形的两边之和大于第三边即可证明.
解答:证明:(1)∵a2+b2=c2,且a,b,c>0,∴(
)2+(
)2=1,
∴0<
<1,0<
<1.
∴当n≥3时,(
)n<(
)2,(
)n<(
)2,
∴(
)n+(
)n<(
)2+(
)2=1,
∴an+bn<cn.
(2)作∠AOB=∠BOC=∠COA=120°,设|OA|=x,|OB|=y,|OC|=z.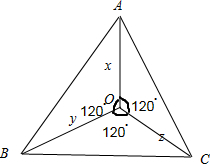
由余弦定理得|AB|=
=
,
同理|BC|=
,|AC|=
.
根据三角形的两边之和大于第三边可得:
|AB|+|BC|>|AC|,
∴
+
>
.
| a |
| c |
| b |
| c |
∴0<
| a |
| c |
| b |
| c |
∴当n≥3时,(
| a |
| c |
| a |
| c |
| b |
| c |
| b |
| c |
∴(
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |
∴an+bn<cn.
(2)作∠AOB=∠BOC=∠COA=120°,设|OA|=x,|OB|=y,|OC|=z.

由余弦定理得|AB|=
| x2+y2-2xycos120° |
| x2+y2+xy |
同理|BC|=
| y2+z2+yz |
| x2+z2+xz |
根据三角形的两边之和大于第三边可得:
|AB|+|BC|>|AC|,
∴
| x2+y2+xy |
| y2+z2+yz |
| z2+x2+xz |
点评:熟练掌握指数函数的单调性、余弦定理、三角形两边之和大于第三边的性质是解题的关键.

练习册系列答案
相关题目
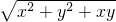 +
+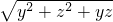 >
>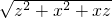 .
.