题目内容
已知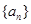 是递增数列,且对
是递增数列,且对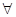
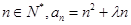 恒成立,则实数λ的取值范围是__________.
恒成立,则实数λ的取值范围是__________.
【答案】
(-3,+∞)
【解析】
试题分析:由{an}是递增数列,得到an+1>an,再由“an=n2+λn恒成立”转化为“λ>-2n-1对于n∈N*恒成立”求解解:∵{an}是递增数列,∴an+1>an,∵an=n2+λn恒成立即(n+1)2+λ(n+1)>n2+λn,∴λ>-2n-1对于n∈N*恒成立.而-2n-1在n=1时取得最大值-3,∴λ>-3,故答案为(-3,+∞)
考点:数列的单调性
点评:本题主要考查由数列的单调性来构造不等式,解决恒成立问题.

练习册系列答案
相关题目
已知
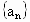 是递增数列,且对任意
是递增数列,且对任意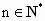 都有
都有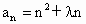 恒成立,则实数λ的取值范围是
恒成立,则实数λ的取值范围是
[
]|
A .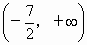 |
B .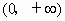 |
|
C .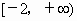 |
D .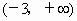 |
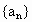 是递增数列,且对任意的nÎ
N*,都有
是递增数列,且对任意的nÎ
N*,都有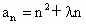 成立,求实数
成立,求实数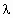 的取值范围.
的取值范围.
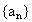 是递增数列,且对任意的nÎ
N*,都有
是递增数列,且对任意的nÎ
N*,都有 成立,求实数
成立,求实数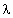 的取值范围.
的取值范围.