题目内容
已知命题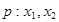 是方程
是方程 的两个实根,不等式
的两个实根,不等式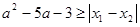 对任意实数
对任意实数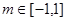 恒成立;命题
恒成立;命题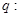 不等式
不等式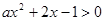 有解,若命题“
有解,若命题“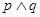 ”为假命题,“
”为假命题,“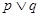 ”为真命题,求实数
”为真命题,求实数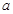 的取值范围.
的取值范围.
【答案】
解:∵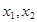 是方程
是方程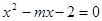 的两个实根,
的两个实根,
∴ 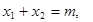
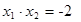
∴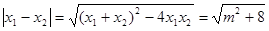 …………2分
…………2分
∴当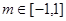 时,
时,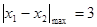 …………3分
…………3分
由不等式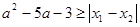 对任意实数
对任意实数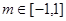 恒成立,可得
恒成立,可得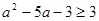
解得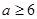 或
或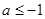
∴命题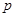 为真命题时,
为真命题时,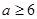 或
或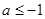 …………5分
…………5分
命题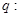 不等式
不等式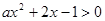 有解
有解
(1)当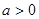 时,显然有解;
时,显然有解;
(2)当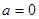 时,
时,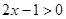 有解
有解
(3)当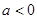 时,∵
时,∵
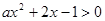 有解,
∴
有解,
∴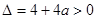 ,有
,有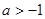
∴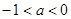
∴命题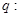 不等式
不等式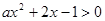 有解时
有解时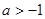 …………10分
…………10分
∵命题“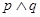 ”为假命题,“
”为假命题,“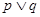 ”为真命题
”为真命题
∴命题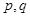 的真假性有两种情况:
的真假性有两种情况: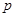 真
真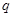 假、
假、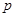 假
假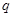 真 …………11分
真 …………11分
当命题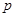 真
真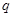 假时,有
假时,有
 ,得
,得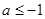 …………12分
…………12分
当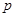 假
假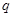 真时,有
真时,有
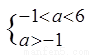 ,得
,得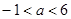 …………13分
…………13分
∴实数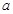 的取值范围为
的取值范围为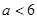 …………14分
…………14分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 三种个体按
三种个体按 的比例分层抽样调查,如果抽取的
的比例分层抽样调查,如果抽取的 个体为9个,则样本容量为30;
个体为9个,则样本容量为30; ,则
,则 每增加1个单位,
每增加1个单位, 平均减少2个单位;
平均减少2个单位; 内的频率为0.4.
内的频率为0.4. :方程
:方程 有两个不相等的实数根;命题
有两个不相等的实数根;命题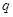 :函数
:函数 是
是 上的单调增函数.若“
上的单调增函数.若“ 的取值范围.
的取值范围.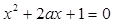 有两个大于-1的实数根,已知命题q:关于x的不等式
有两个大于-1的实数根,已知命题q:关于x的不等式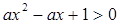 的解集是R,若“p或q”与“
的解集是R,若“p或q”与“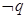 ”
同时为真命题,求实数a的取值范围(12分)
”
同时为真命题,求实数a的取值范围(12分)