题目内容
某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四个月的污染度如表:| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | … |
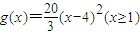 ,
,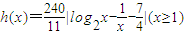 ,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
【答案】分析:(1)通过计算f(1),f(2),f(3),f(4);g(1),g(2),g(3),g(4)和h(1),h(2),h(3),
h(4)的值;可知h(x)更接近表中的实际值,用h(x)模拟较为合理.
(2)由复合函数的单调性知,函数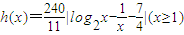 在x≥4上是增函数;且h(23)≈59.6,h(24)≈60.9,知整治后有23个月的污染度不超过60.
在x≥4上是增函数;且h(23)≈59.6,h(24)≈60.9,知整治后有23个月的污染度不超过60.
解答:解:(1)∵f(1)=g(1)=h(1)=60;f(2)=40,g(2)≈26.7,h(2)≈27.3;f(3)=20,g(3)≈6.7,h(3)≈10.9;f(4)=g(4)=h(4)=0;
由此可得h(x)更接近表中的实际值,所以用h(x)模拟比较合理.
(2)因为函数y1=log2x在(x≥4)上是增函数,函数y2=-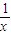 在(x≥4)上是增函数,
在(x≥4)上是增函数,
所以,函数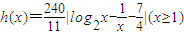 在x≥4上也是增函数;
在x≥4上也是增函数;
又因为h(23)≈59.6,h(24)≈60.9,
故整治后有23个月的污染度不超过60.
点评:本题考查了函数模型的选择与应用问题,选择函数模拟实际问题时,函数值越接近实际值,函数模拟效果越好.
h(4)的值;可知h(x)更接近表中的实际值,用h(x)模拟较为合理.
(2)由复合函数的单调性知,函数
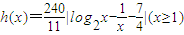 在x≥4上是增函数;且h(23)≈59.6,h(24)≈60.9,知整治后有23个月的污染度不超过60.
在x≥4上是增函数;且h(23)≈59.6,h(24)≈60.9,知整治后有23个月的污染度不超过60.解答:解:(1)∵f(1)=g(1)=h(1)=60;f(2)=40,g(2)≈26.7,h(2)≈27.3;f(3)=20,g(3)≈6.7,h(3)≈10.9;f(4)=g(4)=h(4)=0;
由此可得h(x)更接近表中的实际值,所以用h(x)模拟比较合理.
(2)因为函数y1=log2x在(x≥4)上是增函数,函数y2=-
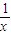 在(x≥4)上是增函数,
在(x≥4)上是增函数,所以,函数
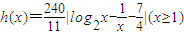 在x≥4上也是增函数;
在x≥4上也是增函数;又因为h(23)≈59.6,h(24)≈60.9,
故整治后有23个月的污染度不超过60.
点评:本题考查了函数模型的选择与应用问题,选择函数模拟实际问题时,函数值越接近实际值,函数模拟效果越好.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四个月的污染度如表:
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:f(x)=20|x-4|(x≥1),g(x)=
(x-4)2(x≥1),h(x)=
|log2x-
-
|(x≥1),其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | 0 | … |
| 20 |
| 3 |
| 240 |
| 11 |
| 1 |
| x |
| 7 |
| 4 |
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四个月的污染度如表:
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:f(x)=20|x-4|(x≥1),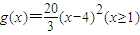 ,
,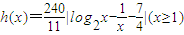 ,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | … |
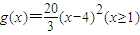 ,
,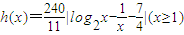 ,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四个月的污染度如表:
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:f(x)=20|x-4|(x≥1), ,
, ,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
| 月数 | 1 | 2 | 3 | 4 | … |
| 污染度 | 60 | 31 | 13 | … |
 ,
, ,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.
,其中x表示月数,f(x)、g(x)、h(x)分别表示污染度.(1)问选用哪个函数模拟比较合理?并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60?
