题目内容
ac>bc是 的条件
的条件
- A.充分不必要
- B.必要不充分
- C.充要
- D.既不充分也不必要
C
分析:根据不等式的基本性质,“ac>bc”一定得出“c≠0”结论,从而c2>0,因为有c2>0这一条件,即可得出 ;反过来若“
;反过来若“ ”,说明c2>0一定成立,一定可以得出“ac>bc”,即可得出答案.
”,说明c2>0一定成立,一定可以得出“ac>bc”,即可得出答案.
解答:∵ac>bc?c≠0
∴c2>0,∴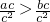 ?
? ;
;
反之,当 时,说明c≠0,
时,说明c≠0,
有c2>0,得ac>bc.
故ac>bc是 的充要条件.
的充要条件.
故选C.
点评:本题以不等式为载体,考查了充分必要条件的判断,充分利用不等式的基本性质是推导不等关系,得出正确结论的重要条件.
分析:根据不等式的基本性质,“ac>bc”一定得出“c≠0”结论,从而c2>0,因为有c2>0这一条件,即可得出
 ;反过来若“
;反过来若“ ”,说明c2>0一定成立,一定可以得出“ac>bc”,即可得出答案.
”,说明c2>0一定成立,一定可以得出“ac>bc”,即可得出答案.解答:∵ac>bc?c≠0
∴c2>0,∴
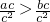 ?
? ;
;反之,当
 时,说明c≠0,
时,说明c≠0,有c2>0,得ac>bc.
故ac>bc是
 的充要条件.
的充要条件.故选C.
点评:本题以不等式为载体,考查了充分必要条件的判断,充分利用不等式的基本性质是推导不等关系,得出正确结论的重要条件.

练习册系列答案
相关题目