题目内容
已知边长为2的正△ABC中，G为△ABC的重心，记
=a，
=b，
=c，则（
+
）•
=
| AB |
| BC |
| CG |
| a |
| b |
| C |
-2
-2
．分析：根据已知中△ABC是边长为2的正三角形，G为△ABC的重心，可得|
|=2，|
|=
，
与
的夹角为150°，由
=
，
=
，
=
，结合向量加法的三角形法则，我们可将(
+
)•
化为
•
，代入向量数量积公式，即可得到答案．
| AC |
| CG |
2
| ||
| 3 |
| AC |
| CG |
| AB |
| a |
| BC |
| b |
| CG |
| c |
| a |
| b |
| c |
| AC |
| CG |
解答：解：∵
=
，
=
，
=
∴(
+
)•
=（
+
）•
=
•
G为△ABC的重心，且△ABC是边长为2的正三角形
故|
|=2，|
|=
，
与
的夹角为150°
∴
•
=|
|•|
|•cos150°=2•
•（-
）=-2
故答案为：-2
| AB |
| a |
| BC |
| b |
| CG |
| c |
∴(
| a |
| b |
| c |
| AB |
| BC |
| CG |
| AC |
| CG |
G为△ABC的重心，且△ABC是边长为2的正三角形
故|
| AC |
| CG |
2
| ||
| 3 |
| AC |
| CG |
∴
| AC |
| CG |
| AC |
| CG |
2
| ||
| 3 |
| ||
| 2 |
故答案为：-2
点评：本题考查的知识点是三角形的重心，向量的数量积公式，向量加法的三角形法则及其几何意义，其中根据条件确定出|
|=2，|
|=
，
与
的夹角为150°，是解答本题的关键．
| AC |
| CG |
2
| ||
| 3 |
| AC |
| CG |
练习册系列答案
名校课堂系列答案
相关题目
已知P是边长为2的正△ABC的边BC上的动点，则
•(
+
)（ ）
| AP |
| AB |
| AC |
| A、最大值为8 | B、是定值6 |
| C、最小值为2 | D、是定值2 |
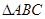边BC上的动点，则
（ ）
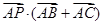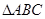的边BC上的动点，则
（ ）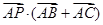