题目内容
函数的图象,如图所示,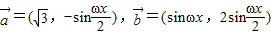 ,则
,则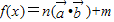 的表达式是(ω>0) .
的表达式是(ω>0) .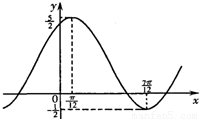
【答案】分析:利用向量的数量积、二倍角公式、两角和的正弦函数化简函数表达式,结合函数的图象求出函数的周期,确定ω,m,n的值,推出函数的表达式.
解答: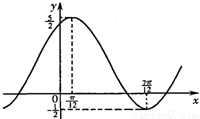 解:
解: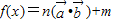 =n
=n +m=
+m=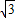 nsinωx-2nsin2
nsinωx-2nsin2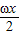 +m
+m
=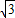 nsinωx+ncos2ωx-1+m=2nsin(ωx+
nsinωx+ncos2ωx-1+m=2nsin(ωx+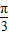 )+m-1,由图象可知函数的周期为:T=
)+m-1,由图象可知函数的周期为:T=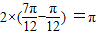 ,所以ω=
,所以ω=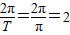 ,
,
m-1=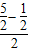 =1,2n=
=1,2n=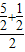 =
= ,所以函数的解析式为:f(x)=
,所以函数的解析式为:f(x)=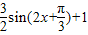 ;
;
故答案为: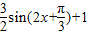 .
.
点评:本题是基础题,考查三角函数的图象,向量的数量积的应用,三角函数的化简,考查计算能力,注意最值的应用,周期的求法.
解答:
 解:
解: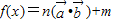 =n
=n +m=
+m=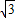 nsinωx-2nsin2
nsinωx-2nsin2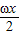 +m
+m=
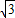 nsinωx+ncos2ωx-1+m=2nsin(ωx+
nsinωx+ncos2ωx-1+m=2nsin(ωx+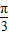 )+m-1,由图象可知函数的周期为:T=
)+m-1,由图象可知函数的周期为:T=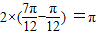 ,所以ω=
,所以ω=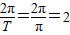 ,
,m-1=
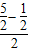 =1,2n=
=1,2n=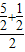 =
= ,所以函数的解析式为:f(x)=
,所以函数的解析式为:f(x)=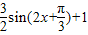 ;
;故答案为:
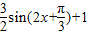 .
.点评:本题是基础题,考查三角函数的图象,向量的数量积的应用,三角函数的化简,考查计算能力,注意最值的应用,周期的求法.

练习册系列答案
相关题目
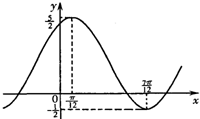
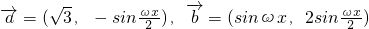 ,则
,则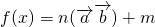 的表达式是(ω>0)________.
的表达式是(ω>0)________.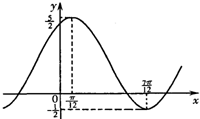
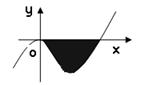
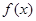 的图象为如图所示的折线段
的图象为如图所示的折线段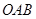 ,其中点
,其中点 的坐标为
的坐标为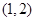 ,点
,点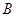 的坐标为
的坐标为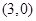 .定义函数
.定义函数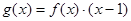 ,则函数
,则函数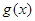 的最大值为
的最大值为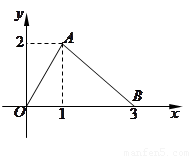
 B.
B. C.
C. D.
D.