题目内容
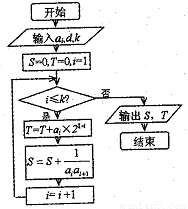
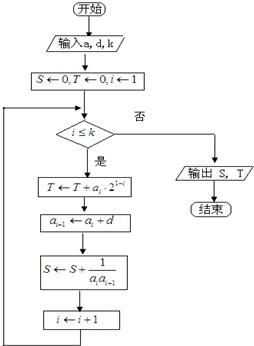 如图所示,流程图给出了无穷整数数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-
如图所示,流程图给出了无穷整数数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-| 5 |
| 9 |
| 10 |
| 99 |
(1)试求数列{an}的通项公式an;
(2)是否存在最小的正数M使得Tn≤M对一切正整数n都成立,若存在,求出M的值;若不存在,请说明理由.
分析:(1)由题意可得
,从而可得
两式相减得:a1(a11-a6)=-90,即a1d=-18又∵a1d=a6所以可求数列通项;
(2)由题意可得Tn=14+
,进一步有当n≥5时,Tn+1-Tn<0;当n≤4时,Tn+1-Tn>0,从而当n=5时,Tn有最大值,进而将问题转化为利用最值解决恒成立问题.
|
|
(2)由题意可得Tn=14+
| 2n-7 |
| 2n-1 |
解答:解:(1)由题设知
又∵{an}是等差数列,设公差为d,
∴
即
两式相减得:a1(a11-a6)=-90,即a1d=-18
又∵a1d=a1(a1+5d)=a12-90,∴a12=81,
∴a1=9,a1=-9舍,∴d=-2,∴an=11-2n
(2)Tn=
+
+
+…+
.①
①式两边同乘
得
Tn=
+
+…+
+
.②
②-①得(1-
)Tn=
+
+
…+
-
.
∴
Tn=9-2(
+
+…+
)-
=9-2(1-
)-
∴Tn=14+
又∵Tn+1-Tn=
-
=
.
当n≥5时,∵Tn+1-Tn<0;当n≤4时,
∵Tn+1-Tn>0∴当n=5时,Tn有最大值
.
∵Tn≤M恒成立,∴M≥
,
∴M的最小值为
.
|
又∵{an}是等差数列,设公差为d,
∴
|
|
两式相减得:a1(a11-a6)=-90,即a1d=-18
又∵a1d=a1(a1+5d)=a12-90,∴a12=81,
∴a1=9,a1=-9舍,∴d=-2,∴an=11-2n
(2)Tn=
| 9 |
| 20 |
| 7 |
| 21 |
| 5 |
| 22 |
| 11-2n |
| 2n-1 |
①式两边同乘
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 21 |
| 7 |
| 22 |
| 13-2n |
| 2n-1 |
| 11-2n |
| 2n |
②-①得(1-
| 1 |
| 2 |
| 9 |
| 20 |
| -2 |
| 21 |
| -2 |
| 22 |
| -2 |
| 2n-1 |
| 11-2n |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 11-2n |
| 2n |
| 1 |
| 2n-1 |
| 11-2n |
| 2n |
∴Tn=14+
| 2n-7 |
| 2n-1 |
又∵Tn+1-Tn=
| 2n-5 |
| 2n |
| 2n-7 |
| 2n-1 |
| 9-2n |
| 2n |
当n≥5时,∵Tn+1-Tn<0;当n≤4时,
∵Tn+1-Tn>0∴当n=5时,Tn有最大值
| 227 |
| 16 |
∵Tn≤M恒成立,∴M≥
| 227 |
| 16 |
∴M的最小值为
| 227 |
| 16 |
点评:本题考查数列、算法与函数的综合问题,本题解题的关键利用错位相减法求数列的和,再用函数的思想来解题,本题是一个综合题目,难度可以作为高考卷的压轴题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 ,
, 时,输出的
时,输出的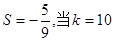 时,输出的
时,输出的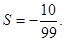 (其中d为公差)
(其中d为公差)
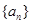 的通项公式;
的通项公式;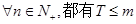 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。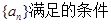 ,
,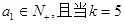 时,输出的
时,输出的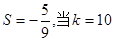 时,输出的
时,输出的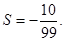 (其中d为公差)
(其中d为公差)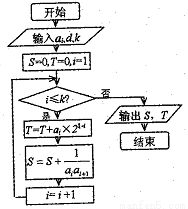
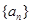 的通项公式;
的通项公式;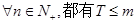 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。 ,
, 时,输出的
时,输出的 时,输出的
时,输出的 (其中d为公差)
(其中d为公差) 的通项公式
的通项公式 成立?若存在,求出m的值,若不存在,请说明理由
成立?若存在,求出m的值,若不存在,请说明理由
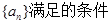 ,
,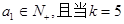 时,输出的
时,输出的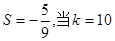 时,输出的
时,输出的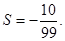 (其中d为公差)
(其中d为公差)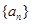 的通项公式
的通项公式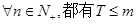 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。