题目内容
一个口袋中装有大小相同的2个白球和3个黑球。
(Ⅰ)从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率。
(Ⅰ)从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率。
解:(Ⅰ)记“摸出两个球,两球恰好颜色不同”为A,摸出两球共有方法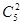 =10种,
=10种,
1分
其中,两球一白一黑有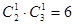 种。 2分
种。 2分
∴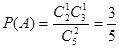 。 4分
。 4分
(Ⅱ)解法一:记摸出一球,放回后再摸出一个球“两球恰好颜色不同”为B,摸出一球得白球的概率为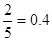 , 5分
, 5分
摸出一球得黑球的概率为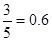 , 6分
, 6分
∴ 。 8分
。 8分
解法二:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”。
∴ 。 6分
。 6分
∴“有放回摸两次,颜色不同”的概率为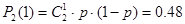 。 8分
。 8分
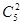 =10种,
=10种,1分
其中,两球一白一黑有
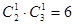 种。 2分
种。 2分∴
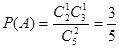 。 4分
。 4分(Ⅱ)解法一:记摸出一球,放回后再摸出一个球“两球恰好颜色不同”为B,摸出一球得白球的概率为
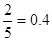 , 5分
, 5分摸出一球得黑球的概率为
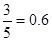 , 6分
, 6分∴
 。 8分
。 8分解法二:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”。
∴
 。 6分
。 6分∴“有放回摸两次,颜色不同”的概率为
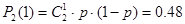 。 8分
。 8分本题考查等可能事件的概率公式,本题解题的关键是写出试验发生包含的事件数和满足条件的事件数,再用公式求解
(Ⅰ)本题是一个等可能事件的概率,摸出两个球共有方法C52种,其中两球一白一黑有6种,得到概率.
(II)摸出一球得白球的概率为2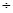 5
5
=0.4,摸出一球得黑球的概率为3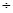 5=0.6,“放回后再摸一次,两球颜色不同”指“先白再黑”或“先黑再白”,这两种情况是互斥的,得到概率
5=0.6,“放回后再摸一次,两球颜色不同”指“先白再黑”或“先黑再白”,这两种情况是互斥的,得到概率
(Ⅰ)本题是一个等可能事件的概率,摸出两个球共有方法C52种,其中两球一白一黑有6种,得到概率.
(II)摸出一球得白球的概率为2
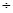 5
5 =0.4,摸出一球得黑球的概率为3
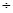 5=0.6,“放回后再摸一次,两球颜色不同”指“先白再黑”或“先黑再白”,这两种情况是互斥的,得到概率
5=0.6,“放回后再摸一次,两球颜色不同”指“先白再黑”或“先黑再白”,这两种情况是互斥的,得到概率
练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
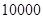 次还能继续使用的概率是
次还能继续使用的概率是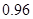 ,开关了
,开关了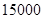 次后还能继续使用的概率是
次后还能继续使用的概率是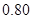 ,则已经开关了
,则已经开关了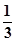
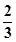
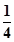
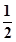
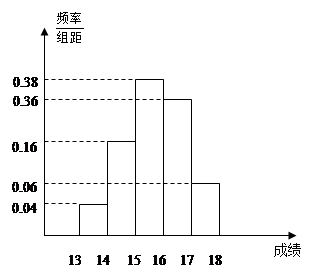
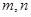 表示该班两位同学百米测试成绩且
表示该班两位同学百米测试成绩且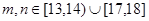 ,求
,求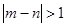 的概率
的概率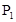 ,乙通过测试的概率为
,乙通过测试的概率为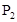 ,则甲、乙至少1人通过测试的概率为( )
,则甲、乙至少1人通过测试的概率为( )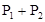
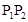
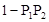
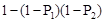
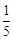
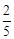
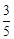
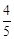
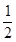 、
、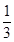 、
、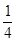 ,则能够将此题解答出的概率为( )
,则能够将此题解答出的概率为( )