题目内容
(本小题满分13分)已知α∈(0,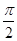 ),且cos2α=
),且cos2α=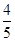 .
.
(Ⅰ)求sinα+cosα的值;
(Ⅱ)若b∈(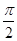 ,π),且5sin(2α+β)=sinβ,求角β的大小 .
,π),且5sin(2α+β)=sinβ,求角β的大小 .
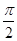 ),且cos2α=
),且cos2α=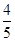 .
.(Ⅰ)求sinα+cosα的值;
(Ⅱ)若b∈(
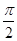 ,π),且5sin(2α+β)=sinβ,求角β的大小 .
,π),且5sin(2α+β)=sinβ,求角β的大小 .解:(I)由cos2α=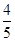 ,得1-2sin2α=
,得1-2sin2α=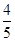 . ……2分
. ……2分
所以sin2α=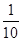 ,又α∈
,又α∈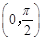 ,所以sinα=
,所以sinα= . ……3分
. ……3分
因为cos2α=1-sin2α,所以cos2α=1- =
=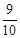 .
.
又α∈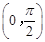 ,所以cosα=
,所以cosα=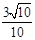 ……5分
……5分
所以sinα+cosα= +
+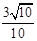 =
=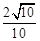 . ……6分
. ……6分
(Ⅱ)因为α∈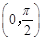 ,所以2α∈
,所以2α∈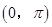 ,
,
由已知cos2α=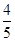 ,所以sin2α=
,所以sin2α=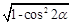 =
= 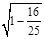 =
= 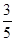 ……7分
……7分
由5sin(2α+β)=sinβ,得5(sin2αcosβ+cos2αsinβ)=sinβ. ……9分
所以5(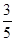 cosβ+sinβ)=sinβ,即3cosβ=-3sinβ,所以tanβ=-1. ……11分
cosβ+sinβ)=sinβ,即3cosβ=-3sinβ,所以tanβ=-1. ……11分
因为β∈ , 所以β=
, 所以β=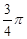 . ……13分
. ……13分
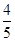 ,得1-2sin2α=
,得1-2sin2α=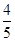 . ……2分
. ……2分所以sin2α=
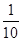 ,又α∈
,又α∈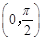 ,所以sinα=
,所以sinα= . ……3分
. ……3分因为cos2α=1-sin2α,所以cos2α=1-
 =
=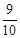 .
.又α∈
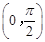 ,所以cosα=
,所以cosα=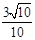 ……5分
……5分所以sinα+cosα=
 +
+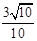 =
=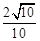 . ……6分
. ……6分(Ⅱ)因为α∈
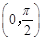 ,所以2α∈
,所以2α∈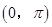 ,
,由已知cos2α=
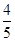 ,所以sin2α=
,所以sin2α=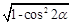 =
= 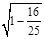 =
= 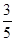 ……7分
……7分由5sin(2α+β)=sinβ,得5(sin2αcosβ+cos2αsinβ)=sinβ. ……9分
所以5(
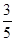 cosβ+sinβ)=sinβ,即3cosβ=-3sinβ,所以tanβ=-1. ……11分
cosβ+sinβ)=sinβ,即3cosβ=-3sinβ,所以tanβ=-1. ……11分因为β∈
 , 所以β=
, 所以β=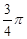 . ……13分
. ……13分略

练习册系列答案
相关题目
 ,存在
,存在 ,使得
,使得 则
则 等于( )
等于( )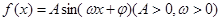 的部分图象如图所示,则
的部分图象如图所示,则 的图象可由函数
的图象可由函数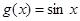 的图象(纵坐标不变)变换如下( )
的图象(纵坐标不变)变换如下( )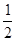 倍,再向右平移
倍,再向右平移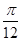 个单位
个单位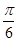 个单位
个单位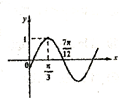
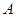 、
、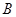 、
、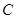 三点的坐标分别是
三点的坐标分别是 ,若
,若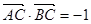 ,则
,则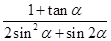 的值为
的值为


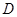 、
、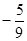
 ,则
,则
 的值等于 .
的值等于 .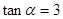 ,则
,则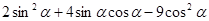 的值为
的值为



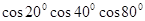 的值为
的值为
 的值为( )
的值为( )



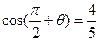 ,则
,则