题目内容
设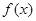 是连续的偶函数,且当
是连续的偶函数,且当 时,
时,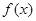 是单调函数,则满足
是单调函数,则满足 的所有
的所有 之和为( )
之和为( )
A. B.
B. C.5 D.
C.5 D.
【答案】
A
【解析】
试题分析:
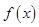 是偶函数
是偶函数


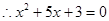 所有x的和为
所有x的和为
考点:函数性质:奇偶性单调性
点评:函数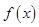 是偶函数则有
是偶函数则有 ,函数
,函数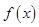 是奇函数则有
是奇函数则有 ,本题中当
,本题中当 时,
时, 是单调函数,所以当
是单调函数,所以当 时函数也是单调函数,
时函数也是单调函数, 方可转化为
方可转化为

练习册系列答案
相关题目
 是连续的偶函数,且当
是连续的偶函数,且当 时,
时,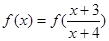 的所有
的所有 的和为 ( )
的和为 ( )