题目内容
一束光线从点A(﹣1,0)出发,经过直线l:2x﹣y+3=0上的一点D反射后,经过点
B(1,0).
(1)求以A,B为焦点且经过点D的椭圆C的方程;
(2)过点B(1,0)作直线l交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围.
B(1,0).
(1)求以A,B为焦点且经过点D的椭圆C的方程;
(2)过点B(1,0)作直线l交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围.
解:(1)点A(﹣1,0)关于直线l:2x﹣y+3=0的对称点为 ,
,
∴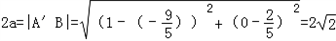 ,c=1,
,c=1,
∴b2=1,
所以所求椭圆方程为: .
.
(2)设直线l:x=my+1,(m∈R),P(x1,y1),Q(x2,y2)
联立方程组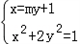 ,
,
消去x得:(my+1)2+2y2=2,即(m2+2)y2+2my﹣1=0,
∴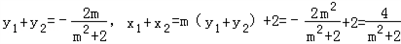
∵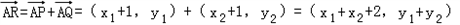
∴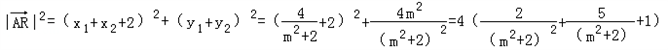 令
令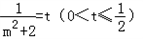 ,则
,则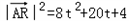 ,
,
∴ .
.
 ,
,∴
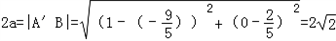 ,c=1,
,c=1,∴b2=1,
所以所求椭圆方程为:
 .
.(2)设直线l:x=my+1,(m∈R),P(x1,y1),Q(x2,y2)
联立方程组
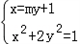 ,
,消去x得:(my+1)2+2y2=2,即(m2+2)y2+2my﹣1=0,
∴
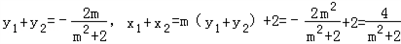
∵
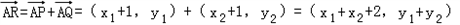
∴
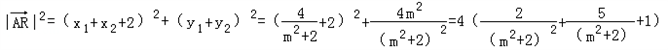 令
令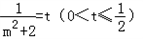 ,则
,则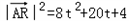 ,
,∴
 .
.
练习册系列答案
相关题目
一束光线从点A(-1,1)出发,经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是( )
A、3
| ||
B、2
| ||
| C、4 | ||
| D、5 |