题目内容
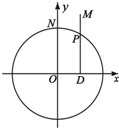 如图:⊙O方程为x2+y2=4,点P在圆上,点D在x轴上,点M在DP延长线上,⊙O交y轴于点N,
如图:⊙O方程为x2+y2=4,点P在圆上,点D在x轴上,点M在DP延长线上,⊙O交y轴于点N,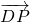 ∥
∥ .且
.且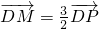 .
.
(I)求点M的轨迹C的方程;
(II)设F1(0, )、F2(0,-
)、F2(0,- ),若过F1的直线交(I)中曲线C于A、B两点,求
),若过F1的直线交(I)中曲线C于A、B两点,求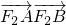 的取值范围.
的取值范围.
解:(I)设P(x0,y0),M(x,y),
∵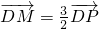 ,∴
,∴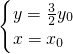 ,∴
,∴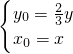 …(3分)
…(3分)
∵⊙O方程为x2+y2=4,点P在圆上,
∴x02+y02=4
∴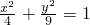
∴点M的轨迹C的方程为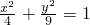 …(5分)
…(5分)
(II)①当直线AB的斜率不存在时,显然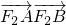 =-4; …(6分)
=-4; …(6分)
②当直线AB的斜率存在时,不妨设AB的方程为:y=kx+ 与椭圆方程联立,消去y可得(9+4k2)x2+8
与椭圆方程联立,消去y可得(9+4k2)x2+8 kx-16=0
kx-16=0
不妨设A(x1,y1),B(x2,y2),则x1+x2=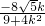 ,x1x2=
,x1x2=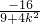
∴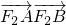 =(1+k2)x1x2+2
=(1+k2)x1x2+2 k(x1+x2)+20=(1+k2)×
k(x1+x2)+20=(1+k2)×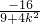 +2
+2 k×
k×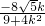 +20=-4+
+20=-4+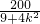 …(10分)
…(10分)
∵9+4k2≥9,∴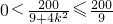
∴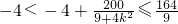
∴ …(11分)
…(11分)
综上所述,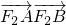 的范围是
的范围是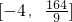 …(12分)
…(12分)
分析:(I)利用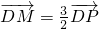 ,确定P,M坐标之间的关系,利用⊙O方程为x2+y2=4,点P在圆上,即可求得点M的轨迹C的方程;
,确定P,M坐标之间的关系,利用⊙O方程为x2+y2=4,点P在圆上,即可求得点M的轨迹C的方程;
(II)①当直线AB的斜率不存在时,显然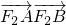 =-4;②当直线AB的斜率存在时,设AB的方程代入椭圆方程,利用韦达定理及向量知识,即可得到结论.
=-4;②当直线AB的斜率存在时,设AB的方程代入椭圆方程,利用韦达定理及向量知识,即可得到结论.
点评:本题考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是联立方程,利用韦达定理进行求解.
∵
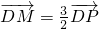 ,∴
,∴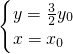 ,∴
,∴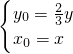 …(3分)
…(3分)∵⊙O方程为x2+y2=4,点P在圆上,
∴x02+y02=4
∴
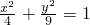
∴点M的轨迹C的方程为
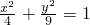 …(5分)
…(5分)(II)①当直线AB的斜率不存在时,显然
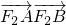 =-4; …(6分)
=-4; …(6分)②当直线AB的斜率存在时,不妨设AB的方程为:y=kx+
 与椭圆方程联立,消去y可得(9+4k2)x2+8
与椭圆方程联立,消去y可得(9+4k2)x2+8 kx-16=0
kx-16=0不妨设A(x1,y1),B(x2,y2),则x1+x2=
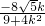 ,x1x2=
,x1x2=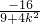
∴
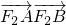 =(1+k2)x1x2+2
=(1+k2)x1x2+2 k(x1+x2)+20=(1+k2)×
k(x1+x2)+20=(1+k2)×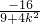 +2
+2 k×
k×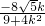 +20=-4+
+20=-4+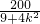 …(10分)
…(10分)∵9+4k2≥9,∴
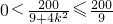
∴
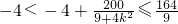
∴
 …(11分)
…(11分)综上所述,
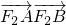 的范围是
的范围是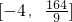 …(12分)
…(12分)分析:(I)利用
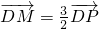 ,确定P,M坐标之间的关系,利用⊙O方程为x2+y2=4,点P在圆上,即可求得点M的轨迹C的方程;
,确定P,M坐标之间的关系,利用⊙O方程为x2+y2=4,点P在圆上,即可求得点M的轨迹C的方程;(II)①当直线AB的斜率不存在时,显然
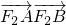 =-4;②当直线AB的斜率存在时,设AB的方程代入椭圆方程,利用韦达定理及向量知识,即可得到结论.
=-4;②当直线AB的斜率存在时,设AB的方程代入椭圆方程,利用韦达定理及向量知识,即可得到结论.点评:本题考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是联立方程,利用韦达定理进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
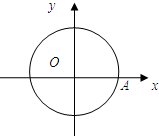 如图,圆O的方程为x2+y2=4,
如图,圆O的方程为x2+y2=4,

 (理)已知函数
(理)已知函数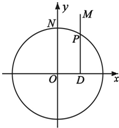 如图:⊙O方程为x2+y2=4,点P在圆上,点D在x轴上,点M在DP延长线上,⊙O交y轴于点N,
如图:⊙O方程为x2+y2=4,点P在圆上,点D在x轴上,点M在DP延长线上,⊙O交y轴于点N,