题目内容
| ∫ | 0 -2 |
| 4-x2 |
分析:本题的求解宜借助图形求定积分,由题意知,此定积分的面积应为半径为2的圆的面积的
| 1 |
| 4 |
解答: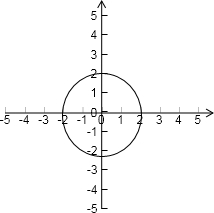 解:令y
解:令y
,x2+y2=4,如图
由定积分的定义知
dx的值等于此圆面第二象限部分的面积
故所求的定积分的值为π
故答案为π
 解:令y
解:令y| 4-x2 |
由定积分的定义知
| ∫ | 0 -2 |
| 4-x2 |
故所求的定积分的值为π
故答案为π
点评:本题考查定积分的定义及其几何意义,求解本题的关键是根据定积分的几何意义将求定积分的问题转化为求几何图形的面积问题.对于一些原函数不易求出的积分问题,利用几何意义求解比较方便.

练习册系列答案
相关题目