题目内容
已知钝角α的顶点在原点,始边与x轴的正半轴重合,终边与单位圆相交于点P(-
,
).
(Ⅰ) 求sin2α-tanα的值;
(Ⅱ) 若函数f(x)=sin(2x-α)cosα-cos(2x-α)sinα,试问该函数y=f(x)的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到.
| ||
| 2 |
| 1 |
| 2 |
(Ⅰ) 求sin2α-tanα的值;
(Ⅱ) 若函数f(x)=sin(2x-α)cosα-cos(2x-α)sinα,试问该函数y=f(x)的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到.
分析:(I)结合三角函数的定义可求sinα,cosα,tanα,然后代入sin2α-tanα=2sinαcosα-tanα
(II)由(I)可求α,然后代入f(x)=sin(2x-α)cosα-cos(2x-α)sinα=sin(2x-2α)=sin(2x-
),结合正弦函数的图象的变换即可求解
(II)由(I)可求α,然后代入f(x)=sin(2x-α)cosα-cos(2x-α)sinα=sin(2x-2α)=sin(2x-
| 5π |
| 3 |
解答:解:(I)由三角函数的定义可得,sinα=
,cosα=-
,tanα=-
…(3分)
∴sin2α-tanα=2sinαcosα-tanα=-
+
=-
…(6分)
(II)由(I)可得,α=
∴f(x)=sin(2x-α)cosα-cos(2x-α)sinα=sin(2x-2α)
=sin(2x-
)(8分)
∴函数y=f(x)的图象可由y=sinx的图象先向右平移
个单位,然后把函数的图象上的纵坐标不变,横坐标缩短到原来的
即可得到…(14分)
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
∴sin2α-tanα=2sinαcosα-tanα=-
| ||
| 2 |
| ||
| 3 |
| ||
| 6 |
(II)由(I)可得,α=
| 5π |
| 6 |
∴f(x)=sin(2x-α)cosα-cos(2x-α)sinα=sin(2x-2α)
=sin(2x-
| 5π |
| 3 |
∴函数y=f(x)的图象可由y=sinx的图象先向右平移
| 5π |
| 3 |
| 1 |
| 2 |
点评:本题主要考查了三角函数的定义,三角函数的图象的平移及周期的变化,属于正弦函数的简单应用.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
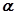 的顶点在原点,始边与
的顶点在原点,始边与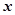 轴的正半轴重合,终边与单位圆相交于点
轴的正半轴重合,终边与单位圆相交于点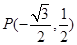 .
. 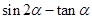 的值;
的值;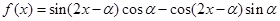 ,
试问该函数
,
试问该函数 的图象可由
的图象可由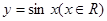 的图象经过怎样的平移和伸缩变换得到.
的图象经过怎样的平移和伸缩变换得到. 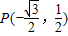 .
.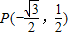 .
.