题目内容
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中
(1)求 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)设函数函数g(x)= 
 ;试比较g(x)与
;试比较g(x)与 的大小。
的大小。
【答案】
(1) 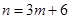
(2) 当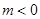 时,
时,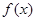 在
在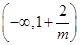 单调递减,在
单调递减,在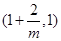 单调递增,在
单调递增,在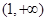 上单调递减.同理可得:当
上单调递减.同理可得:当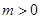 时,
时,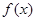 在
在 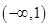 单调递增,在
单调递增,在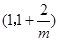 单调递减,在
单调递减,在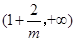 上单调递增
上单调递增
(3) 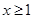 时 ,g(x)
时 ,g(x)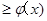
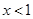 时, g(x)
时, g(x)
【解析】
试题分析:解(I)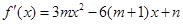 因为
因为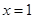 是函数
是函数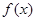 的一个极值点,所以
的一个极值点,所以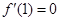 ,即
,即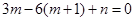 ,所以
,所以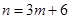 3分
3分
(II)由(I)知,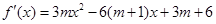 =
=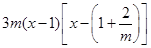 …5分
…5分
当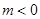 时,有
时,有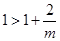 ,当
,当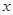 变化时,
变化时,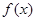 与
与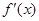 的变化如下表:
的变化如下表:
|
|
|
|
|
1 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
调调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
故有上表知,当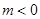 时,
时,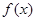 在
在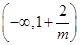 单调递减,在
单调递减,在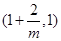 单调递增,在
单调递增,在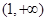 上单调递减.同理可得:当
上单调递减.同理可得:当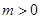 时,
时,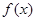 在
在 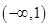 单调递增,在
单调递增,在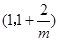 单调递减,在
单调递减,在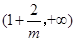 上单调递增. 9分
上单调递增. 9分
(III)设函数h(x)=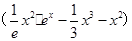 -
-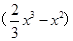 =
=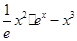 =
=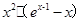
由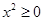 ,且
,且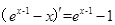 ,故
,故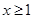 ,
,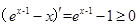
令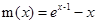 所以m(x)在
所以m(x)在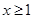 为增函数,故
为增函数,故
所以h(x)在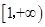 ,h(x)
,h(x)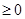 ,故g(x)
,故g(x)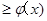
当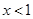 ,
,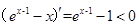
令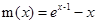 所以m(x)在
所以m(x)在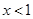 为减函数,故
为减函数,故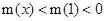
所以h(x)在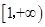 ,h(x)
,h(x)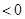 ,故g(x)
,故g(x)
综上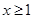 时 ,g(x)
时 ,g(x)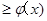 14分
14分
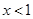 时, g(x)
时, g(x)
考点:导数的运用
点评:解决的关键是利用导数的符号与函数单调性的关系来确定单调性,以及极值问题,并利用单调性来比较大小,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
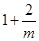
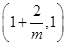
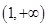
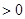
 是函数
是函数 的一个极值点.
的一个极值点.
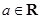

 的值;
的值; ,
, 时,证明:
时,证明:
 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与 的关系式;
的关系式;  的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求
,求 的取值范围.
的取值范围. 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 。
。 与
与 的关系表达式;
的关系表达式; 的单调区间;
的单调区间; 时,函数
时,函数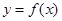 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求实数
,求实数 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与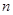 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3