题目内容
记函数f（x）=f1（x），f（f（x））=f2（x），它们定义域的交集为D，若对任意的x∈D，f2（x）=x，则称f（x）是集合M的元素，例如f（x）=-x+1，对任意x∈R，f2（x）=f（f（x））=-（-x+1）+1=x，故f（x）=-x+1∈M．
（1）设函数f（x）=log2（1-2x），判断f（x）是否是M的元素，并求f（x）的反函数f-1（x）；
（2）
（a＜0），求使f（x）＜1成立的x的范围．
【答案】分析：（1）根据题中的定义判断f（x）是否是M的元素即可．再求得f（x）的反函数f-1（x）；
（2）根据定义，问题可转换为f2（x）=f（f（x））=x对一切定义域中x恒成立．
，从而可得：（a+b）x2-（a2-b2）x=0恒成立，即a+b=0，故可解不等式，即可求使f（x）＜1成立的x的范围．
解答：解：（1）∵
∴f（x）=log2（1-2x）∈M
设y=log2（1-2x）
由0＜1-2x＜1解得：x＜0，y＜0
由y=log2（1-2x）得2y=1-2x，反函数为y=loga（1-ax），（x＜0）
（2）∵
，
∴f2（x）=f（f（x））=x对一切定义域中x恒成立．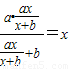
，
解得：（a+b）x2-（a2-b2）x=0恒成立，故a+b=0
由f（x）＜1，得到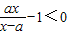
，
，由a＜0，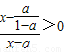
，
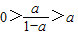故x的范围为：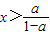
或 x＜a
点评：本题以函数为载体，考查新定义，根据是对新定义的理解，同时考查学生等价转化问题的能力．
（2）根据定义，问题可转换为f2（x）=f（f（x））=x对一切定义域中x恒成立．
，从而可得：（a+b）x2-（a2-b2）x=0恒成立，即a+b=0，故可解不等式，即可求使f（x）＜1成立的x的范围．解答：解：（1）∵
∴f（x）=log2（1-2x）∈M
设y=log2（1-2x）
由0＜1-2x＜1解得：x＜0，y＜0
由y=log2（1-2x）得2y=1-2x，反函数为y=loga（1-ax），（x＜0）
（2）∵
，∴f2（x）=f（f（x））=x对一切定义域中x恒成立．
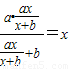，解得：（a+b）x2-（a2-b2）x=0恒成立，故a+b=0
由f（x）＜1，得到
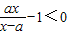，，由a＜0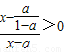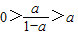，，故x的范围为：
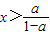或 x＜a点评：本题以函数为载体，考查新定义，根据是对新定义的理解，同时考查学生等价转化问题的能力．
练习册系列答案
全优点练单元计划系列答案
相关题目