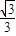Question

计算cos 28° cos17°-sin 28° sin17°的结果等于（　　）

• A、

  1

  2

• B、

  2

  2

• C、

  3

  2

• D、

  3

  3

Answer 1

分析：把所求的式子利用两角和的余弦函数公式化简，然后再利用特殊角的三角函数值即可求出值．

解答：解：cos 28° cos17°-sin 28° sin17°
=cos（28°+17°）
=cos45°=

2

2

．
故选B

点评：此题考查学生灵活运用两角和的余弦函数公式及特殊角的三角函数值化简求值，是一道基础题．