题目内容
(本小题8分) 设函数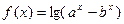 (常数
(常数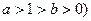
(1)求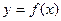 的定义域;
的定义域;
(2)在函数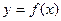 的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
(3)当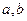 满足什么条件时,
满足什么条件时,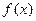 在
在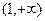 上恒取正值。
上恒取正值。
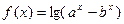 (常数
(常数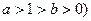
(1)求
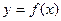 的定义域;
的定义域;(2)在函数
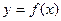 的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?(3)当
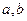 满足什么条件时,
满足什么条件时,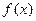 在
在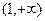 上恒取正值。
上恒取正值。 (1)定义域为
(1)定义域为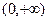 (2)
(2)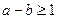
解:(1)定义域为
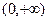
(2)通过定义可证函数
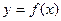 在定义域上是单调递增的,所以不存在不同的两点,使得过这两点的直线平行于x轴。
在定义域上是单调递增的,所以不存在不同的两点,使得过这两点的直线平行于x轴。(3)由于函数在定义域上单调递增,所以只需
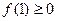 即可,解得
即可,解得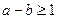 .
.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
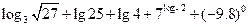 。
。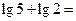 _______________
_______________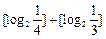
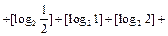
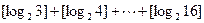 的值为
的值为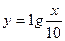 的图象,可以把函数
的图象,可以把函数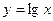 的图象( )
的图象( )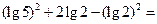
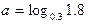 ,
,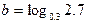 ,
,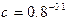 ,则( )
,则( )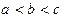
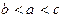
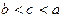
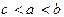
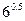 ,
,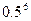 ,
,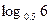 的大小顺序为 ( )
的大小顺序为 ( )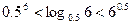 (B)
(B)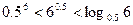
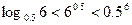 (D)
(D)