��Ŀ����
���壺������y=f��x����ijһ����D����ȡ����ʵ��x1��x2����x1��x2������
��f(
)����ƺ���y=f��x��������D�Ͼ�������L��
��1��д��һ�����䶨�����Ͼ�������L�Ķ�����������Ҫ��֤������
��2�����ں���f(x)=x+
���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�
��3��������f(x)=
-ax2�����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
��1��д��һ�����䶨�����Ͼ�������L�Ķ�����������Ҫ��֤������
��2�����ں���f(x)=x+
| 1 |
| x |
��3��������f(x)=
| 1 |
| x |
��������1��д���ĺ������°��ĺ������ɣ�
��2������f(x)=x+
�����䣨0��+�ޣ��Ͼ�������L�����ݶ��壬��ȡx1��x2�ʣ�0��+�ޣ�����x1��x2
ֻ��Ҫ֤��
-f(
)��0���ɣ�
��3����ȡx1��x2�ʣ�0��1������x1��x2��
-f(
)��0��ֻ��Ҫ2-a•x1•x2��x1+x2����0��x1��x2�ʣ�0��1���Ϻ��������a��
���ʿ���ʵ��a��ȡֵ��Χ��
��2������f(x)=x+
| 1 |
| x |
ֻ��Ҫ֤��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
��3����ȡx1��x2�ʣ�0��1������x1��x2��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 2 |
| x1•x2(x1+x2) |
����⣺��1��y=log
x�����������ڣ�0��1���ϵĶ���������������2�֣�
��2������f(x)=x+
�����䣨0��+�ޣ��Ͼ�������L������4�֣�
֤������ȡx1��x2�ʣ�0��+�ޣ�����x1��x2
��
-f(
)=
(x1+
+x2+
)-(
+
)=
•
-
=
=
��x1��x2�ʣ�0��+�ޣ���x1��x2��
�ࣨx1-x2��2��0��2x1•x2��x1+x2����0
��
-f(
)��0��
��
��f(
)
���Ժ���f(x)=x+
�����䣨0��+�ޣ��Ͼ�������L������8�֣�
��3����ȡx1��x2�ʣ�0��1������x1��x2
��
-f(
)=
(
-ax12+
-ax22)-(
-a(
)2)=
-a•
=(x1-x2)2•
��x1��x2�ʣ�0��1����x1��x2��
�ࣨx1-x2��2��0��4x1•x2��x1+x2����0
Ҫʹ��ʽ�����㣬����2-a•x1•x2��x1+x2����0��x1��x2�ʣ�0��1���Ϻ������
��a��
��
��a��1��
��ʵ��a��ȡֵ��ΧΪ��-�ޣ�1]����14�֣�
| 1 |
| 2 |
��2������f(x)=x+
| 1 |
| x |
֤������ȡx1��x2�ʣ�0��+�ޣ�����x1��x2
��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| 1 |
| 2 |
| x1+x2 |
| x1•x2 |
| 2 |
| x1+x2 |
| (x1+x2)2-4x1•x2 |
| 2x1•x2(x1+x2) |
| (x1-x2)2 |
| 2x1•x2(x1+x2) |
��x1��x2�ʣ�0��+�ޣ���x1��x2��
�ࣨx1-x2��2��0��2x1•x2��x1+x2����0
��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
���Ժ���f(x)=x+
| 1 |
| x |
��3����ȡx1��x2�ʣ�0��1������x1��x2
��
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| 2 |
| x1+x2 |
| x1+x2 |
| 2 |
| (x1-x2)2 |
| 2x1•x2(x1+x2) |
| (x1-x2)2 |
| 4 |
| [2-a•x1•x2(x1+x2)] |
| 4x1•x2(x1+x2) |
��x1��x2�ʣ�0��1����x1��x2��
�ࣨx1-x2��2��0��4x1•x2��x1+x2����0
Ҫʹ��ʽ�����㣬����2-a•x1•x2��x1+x2����0��x1��x2�ʣ�0��1���Ϻ������
��a��
| 2 |
| x1•x2(x1+x2) |
��a��1��
��ʵ��a��ȡֵ��ΧΪ��-�ޣ�1]����14�֣�
�����������Ժ���Ϊ���壬�����¶��壬�����������⣬����Ĺؼ��Ƕ��¶�������⣬�����������÷����������

��ϰ��ϵ�д�
�����Ŀ
 ����ƺ���y=f��x��������D�Ͼ�������L��
����ƺ���y=f��x��������D�Ͼ�������L�� ���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�
���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�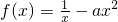 �����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��
�����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��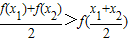 ����ƺ���y=f��x��������D�Ͼ�������L��
����ƺ���y=f��x��������D�Ͼ�������L��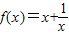 ���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�
���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�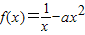 �����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��
�����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��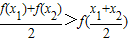 ����ƺ���y=f��x��������D�Ͼ�������L��
����ƺ���y=f��x��������D�Ͼ�������L��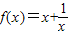 ���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�
���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�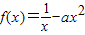 �����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��
�����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��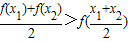 ����ƺ���y=f��x��������D�Ͼ�������L��
����ƺ���y=f��x��������D�Ͼ�������L�� ���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ�
���ж��������䣨0��+�ޣ����Ƿ��������L��������������֤����Ľ��ۣ� �����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��
�����䣨0��1���Ͼ�������L����ʵ��a��ȡֵ��Χ��